A particle is fired vertically upward with a speed $v_{0}$ . Find
(a) Speed at distance $2 R_{e}$ from centre of earth.
(b) Calculated maximum height attained by particle.

Video Solution

Text Solution

Verified by Experts

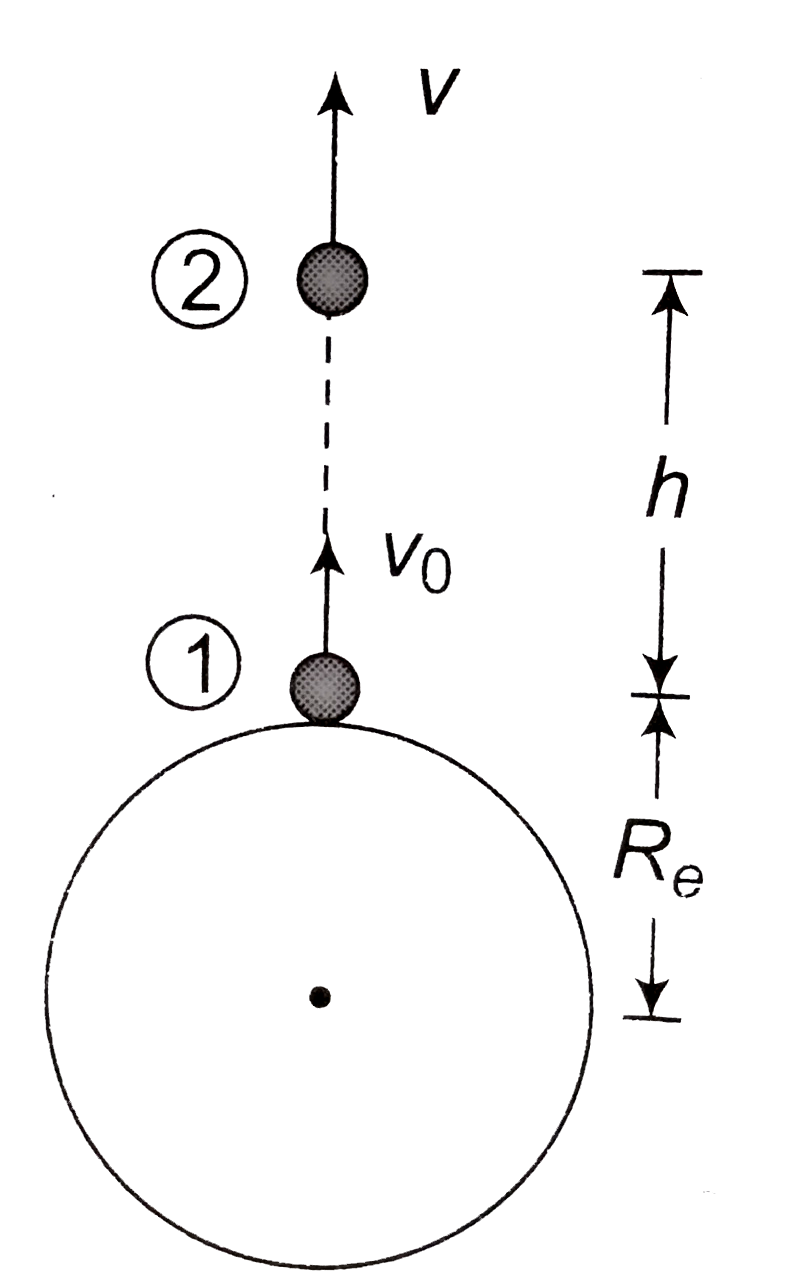
Applying energy conservation between $(1)$ and $(2)$
$K_{1} + U_{1} = K_{2} + U_{2}$
$\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} = \frac{1}{2} m v^{2} - \frac{G M_{e} m}{(R_{e} + h)}$
$R_{e} + h = 2 R_{e}$
$\frac{1}{2} m v^{2} = \frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} + \frac{G M_{e} m}{2 R_{e}}$
$\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{2 R_{e}}$
$v^{2} = v_{0}^{2} - \frac{G M_{e}}{R_{e}}$
$v = {(v_{0} - \frac{G M_{e}}{R_{e}})}_{0}^{1 / 2} = {(v_{0}^{2} - g R_{e}^{2})}^{1 / 2}$
(b) $h = H_{max}$ if $v = 0$
$\frac{1}{2} m v_{0}^{2} = G M_{e} m [\frac{1}{R_{e}} - \frac{1}{R_{e} + h}]$
$\frac{v_{0}^{2}}{2 G M_{e}} = \frac{h}{R_{e} (R_{e} + h)}$
$\frac{h}{(R_{e} + h)} = \frac{v_{0}^{2} R_{e}}{2 G M_{e}} = \frac{v_{0}^{2} R_{e}}{2 g R_{e}^{2}} = \frac{v_{0}^{2}}{2 g R_{e}}$
$\frac{R_{e} + h}{h} = \frac{2 g R_{e}}{v_{0}^{2}}$
$\frac{R_{e}}{h} + 1 = \frac{2 g R_{e}}{v_{0}^{2}}$
$\frac{R_{e}}{h} = \frac{2 g R_{e}}{v_{0}^{2}} - 1$
$h = \frac{R_{e}}{(\frac{2 g R_{e}}{v_{0}^{2}} - 1)} = \frac{V_{0}^{2} R_{e}}{(2 g R_{e} - v_{0}^{2})}$

Updated on:21/07/2023

A particle is projected vertically upwards in vacuum with a speed $u$ .
AWhen it rises to half its maximum height, its speed becomes $u / 2$ .
BWhen it rises to half its maximum height, its speed becomes $u / \sqrt{2}$ .
CThe time taken to rise to half its maximum height is half the time taken to reach its maximum height.
DThe time taken to rise to three $-$ fourth of its maximum height is half the time taken to reach its maximum height.
A particle is prjected vertically upwards the surface of the earth (radius $R_{e})$ with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
A $\frac{16}{15} R_{e}$
B $\frac{R_{e}}{15}$
C $\frac{4}{15} R_{e}$
DNone of these
A particle is projected vertically upwards with a velocity $\sqrt{g R}$ , where $R$ denotes the radius of the earth and $g$ the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
A $R_{e}$
B $2 R_{e}$
C $\frac{R_{e}}{2}$
DNone of these