Two blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
r=0.3m,r1=0.124m,r2=r−r1=0.176m
T=m2r2ω2=5×(0.176)×(10)2=88N
T+f=m1ω2r1
88+f=10×(10)2×0.124=124
f=36N
Friction on m1:36N
(b) Considering (m−(1)+m2) as system
=m2r2ω2
T+f=m1r1ω2
f=(m1r1−m2r2)ω2
Mass will slip if
(m1r1−m2r2)ω2>fmax(=μm1g)
ωmin=√μm1gm1r1−m2r2=11.67rad/s
(c ) When f=0⇒m1r1=m2r2⇒10r1=5r−(2)
r2=2r1
r1+r2=0.3⇒r1=0.1m,r2=0.2m

Topper's Solved these Questions
Similar Questions
A particle revolves round a circular path with a constant speed.
(i) the velecity of the particle is along the tangent.
(ii) the acceleration of the particle of the particle is always towards center.
(iii) the magnetic of acceleration is constant.
(iv) The work done by the centripetal force is always zero.
View SolutionTwo blocks of mass 1kg and 3kg have position v ectors ˆi+2ˆj+ˆk and 3ˆi−2ˆj+ˆk , respectively . The center of mass of this system has a position vector.
View SolutionIn making an alloy, a substance of specific gravity s1 and mass m1 is mixed with another substance of specific gravity of the alloy is
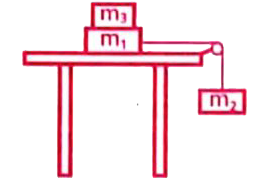
View SolutionThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?
View SolutionThere are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View SolutionTwo blocks of masses m_(1) and m_(2) are connected through a massless inextensible string .A block of mass m_(1) is placed at the fixed rigid inclined surface while the block of mass m_(2) hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m_(1) and m_(2) released from rest
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View Solutionm1,m2 व m3 द्रव्यमान के तीन पिण्ड क्रमागत द्रव्यमान रहित डोरी से जुड़े हैं और एक घर्षण रहित मेज पर रखे हैं | यदि m3 द्रव्यमान को बल F से खींचा जाए, तो m2 व m3 द्रव्यमानों के बीच डोरी में तनाव होगा :
View SolutionIn the arragement of figure assume negligible friction between the blocks and table. If F the pulling force and m_(1) and m_(2) the masses are known, then the tension in the string is :
View SolutionIn the arrangement of figure assume negligible friction between the blocks and table. If F the pulling force and m_(1) and m_(2) the masses are known, then the tension in the string is–
View Solutionm1=10kg व m2=5kg के दो ब्लॉक 0.3m की द्र्व्यमाणहीन अविस्तर्य डोरी द्वारा एक दूसरे से संयोजित है, एक घूमने योग्य टेबल के व्यास के अनुदिश स्थित है । टेबल व m1 के मध्य घर्षण गुणांक 0.5 है जबकि m2 व टेबल के मध्य कोई घर्षण नहीं है । टेबल इसके केंद्र से गुजर रही ऊर्ध्वाधर अक्ष के पारित 10rad/sec कोणीय वेग से घूर्णन कर रही है । दोनों कण द्रव्यमान केंद्र O के एक और टेबल के व्यास के अनुदिश इस प्रकार रखे हुए है की m1,O से 0.124m की दुरी पर है । दोनों द्रव्यमान घूर्णन टेबल पर प्रेक्षक के सापेक्ष विरामावस्था में प्रेक्षित होते है।
(i) m1 पर घर्षण बल की गणना कीजिये।
(ii) घूर्णन टेबल की न्यूनतम कोणीय चाल क्या होनी चाहिए ताकि द्रव्यमान इस स्थिति से फिसले।
(iii) डोरी को तनी हुई रहने के लिए द्रव्यमान को कहा स्थित होना चाइये ताकि m1 द्रव्यमान पर कोई घर्षण बल कार्यरत नहीं हो।
View SolutionTwo masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the corner of the table as shown in the the coefficent of static friction of mass m1 with the table is μs calculate the minium mass m3 that may be placed on m1 to prevent it from sliding check if m1=15kgm2=10kg,mm3=25 and μs=0.2
View SolutionA round table is rotated with an angular velocity of 10 rad cdot s^(-1) about its axis. Two blocks of mass m_(1) = 10 kg and m_(2) = 5 kg , connected to each other by a weightless inextensible string of length 0.3 m, are placed along a diameter of the table. the coefficient of friction between the table and m_(1) is 0.5, while there is no frication between m_(2) and the table. Mass m_(1) is at a distance of 0.124 m from the centre of the table. The masses are at rest with respect to the table. (i) Calculate the frictional force on m_(1) . (ii) What should be the minimum angular speed of the table so that masses will slip from the table? (iii) how should these masses be kept so that the string remains taut but no frictional force acts on m_(1) ?
View Solutionm1=10kg व m2=5kg के दो ब्लॉक 0.3m की द्र्व्यमाणहीन अविस्तर्य डोरी द्वारा एक दूसरे से संयोजित है, एक घूमने योग्य टेबल के व्यास के अनुदिश स्थित है । टेबल व m1 के मध्य घर्षण गुणांक 0.5 है जबकि m2 व टेबल के मध्य कोई घर्षण नहीं है । टेबल इसके केंद्र से गुजर रही ऊर्ध्वाधर अक्ष के पारित 10rad/sec कोणीय वेग से घूर्णन कर रही है । दोनों कण द्रव्यमान केंद्र O के एक और टेबल के व्यास के अनुदिश इस प्रकार रखे हुए है की m1,O से 0.124m की दुरी पर है । दोनों द्रव्यमान घूर्णन टेबल पर प्रेक्षक के सापेक्ष विरामावस्था में प्रेक्षित होते है।
(i) m1 पर घर्षण बल की गणना कीजिये।
(ii) घूर्णन टेबल की न्यूनतम कोणीय चाल क्या होनी चाहिए ताकि द्रव्यमान इस स्थिति से फिसले।
(iii) डोरी को तनी हुई रहने के लिए द्रव्यमान को कहा स्थित होना चाइये ताकि m1 द्रव्यमान पर कोई घर्षण बल कार्यरत नहीं हो।
View SolutionThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?
View Solution

