A particle of mass $m$ is attacted to one end of string of length $3 L$ . The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other end is attached to a small particle of mass $m_{0}$ . The particle describe horizontal circular motion with angular velocity $ω_{1}$ and $ω_{2}$ . find the value of (a) $\frac{ω_{1}}{ω_{2}}$ and (b) the value of $(\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2}})$ .

Video Solution

Text Solution

Verified by Experts

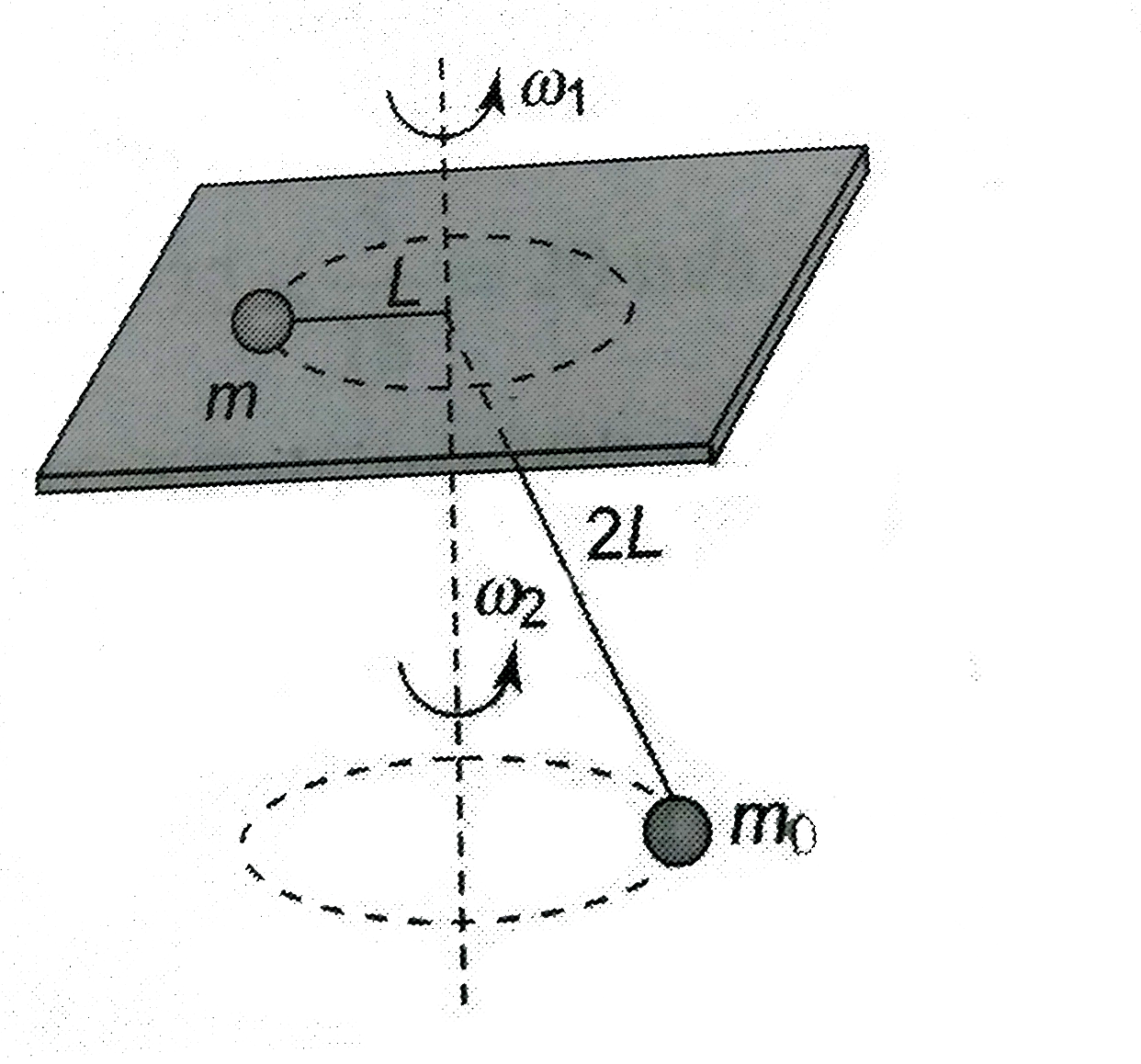
For the block on table: $T = m ω - {(1)}^{2} L$ ….. $(i)$
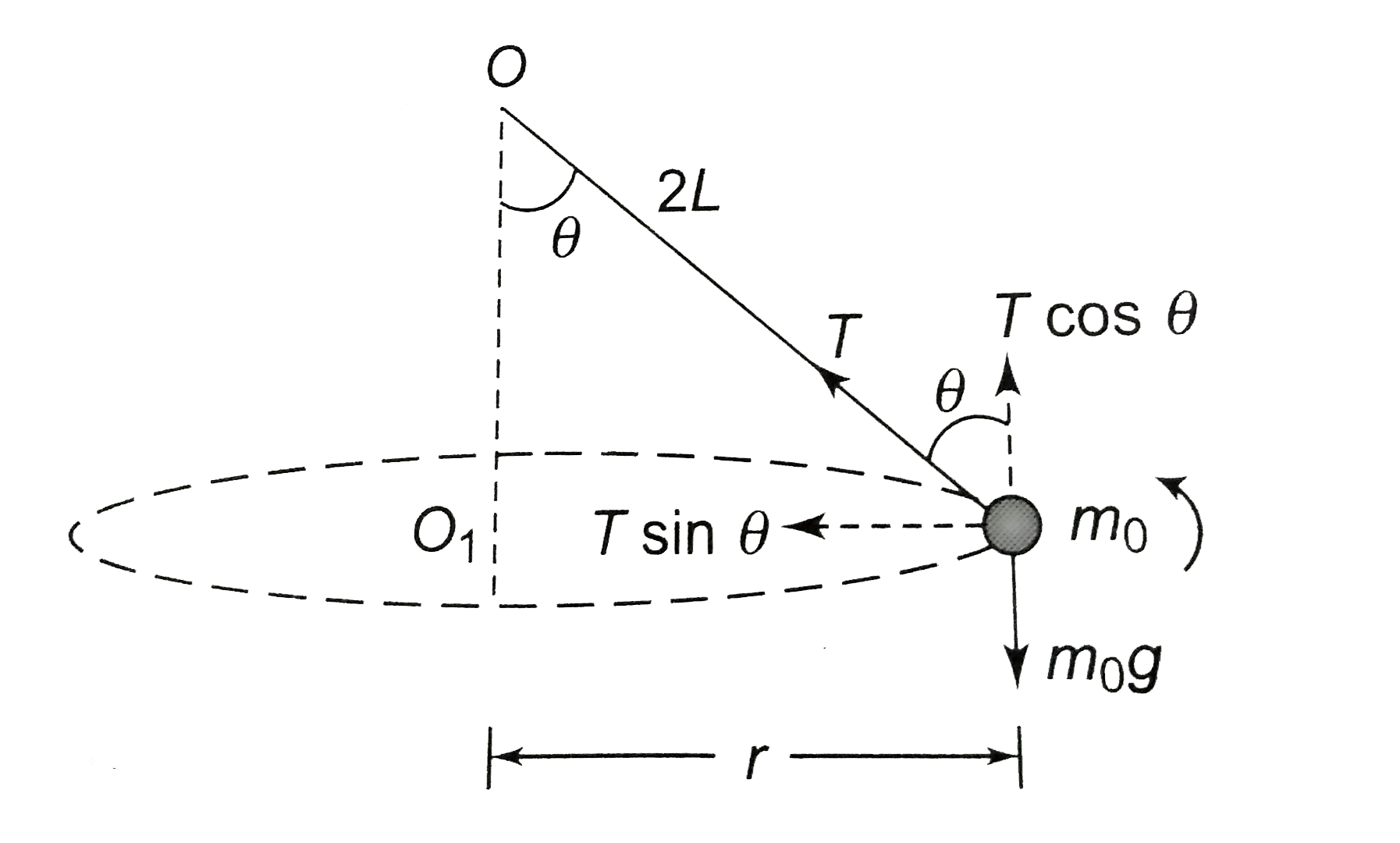
For hanging mass: $sin θ = \frac{r}{2 L}$ …. $(i i)$
$T cos θ = m_{0} g$ … $(i i i)$
$T sin θ = m_{0} ω_{2}^{2} r$ ….. $(i v)$
$T sin θ = m_{0} ω_{2}^{2} 2 L sin θ$
$T = m_{0} ω_{2}^{2} 2 L$ ..... $(v)$
Equating $(i)$ and $(v)$ , we get
$m ω_{1}^{2} L = m_{0} ω_{2}^{2} 2 L$
$\frac{ω_{1}^{2}}{ω_{2}^{2}} = 2 \frac{m_{0}}{m} \Rightarrow ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ \frac{ω_{1}}{ω_{2} = \sqrt{(2 \frac{m_{0}}{m})}}$
From $(i)$ , $\frac{1}{ω_{1}^{2}} = \frac{m L}{T}$
From $(v)$ , $\frac{1}{ω_{2}^{2} = \frac{2 m_{0} L}{T}}$
$\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2}} = \frac{L}{T} [m + 2 m_{0}]$
From $(i i i)$ , $T = \frac{m_{0} g}{cos θ}$
$\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2}} = \frac{L cos θ}{m_{0} g} [m + 2 m_{0}]$
Since $cos θ < 1, t h e r e f o r e$
$(\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2}}) < \frac{L}{g} [\frac{m}{m_{0}} + 2]$

Updated on:21/07/2023

A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
A $\frac{r g}{\sqrt{L^{2} - r^{2}}}$
B $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
C $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A $\sqrt{\frac{T l}{m}}$
B $\sqrt{\frac{2 T l}{m}}$
C $\sqrt{\frac{3 T l}{m}}$
D $\sqrt{\frac{T}{m l}}$
A particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A $2 π \sqrt{g h}$
B $\sqrt{g / h}$
C $2 π \sqrt{h / g}$
D $\frac{1}{2 π} \sqrt{g / h}$