Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.

Video Solution

Text Solution

Verified by Experts

Let particle is at equilibrium position at $t = 0$
$x = A sin (ω t + ϕ)$
At $t = 0, x = 0$ i.e., $sin (ϕ) = 0 \Rightarrow ϕ = 0$
$x = A sin ω t$

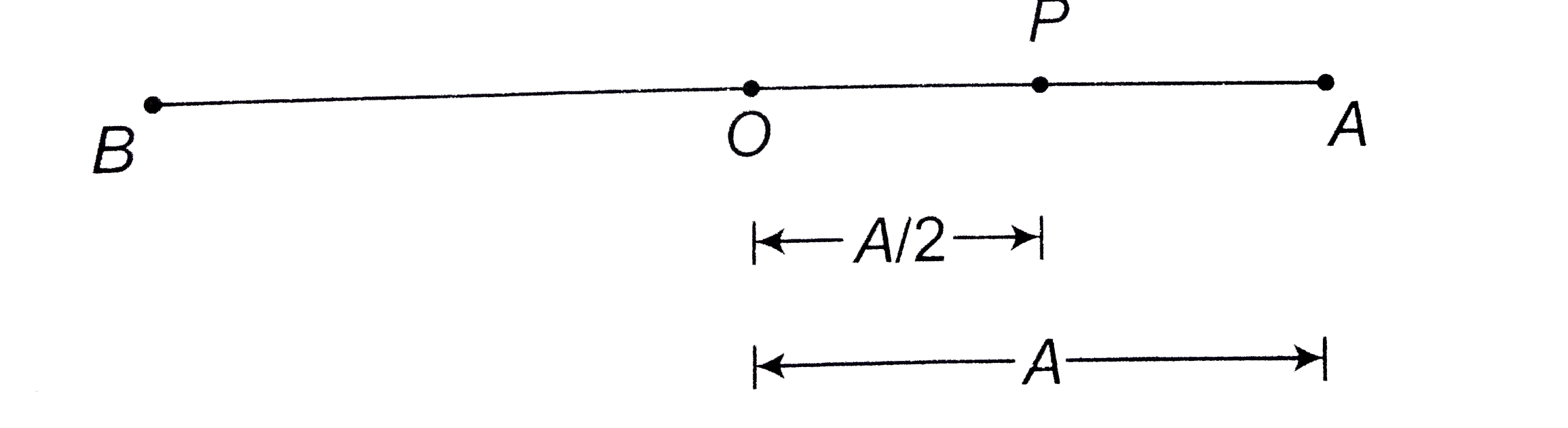
Time taken by particle to move from O to P i.e., $x = A / 2$
$x = A sin ω t \Rightarrow \frac{A}{2} = A sin ω t$
$sin ω t = \frac{1}{2} = sin π / 6$
$ω t = π / 6 \Rightarrow \frac{2 π}{T} t = \frac{π}{6} \Rightarrow t = \frac{T}{12}$
Time taken by particle to move from O to A $= T / 4$
Time from P to A i.e., $x = A / 2$ to $x = A$
$= T / 4 - T / 12 = T / 6$

Updated on:21/07/2023

A simple harmonic motion of amplitude A has a time period T. The acceleration of the oscillator when its displacement is half the amplitude is
A $\frac{4 π^{2} A}{T^{2}}$
B $\frac{2 π^{2} A}{T^{2}}$
C $- \frac{4 π^{2} A}{T^{2}}$
D $- \frac{2 π^{2} A}{T^{2}}$
A simple harmonic oscillator has time period T. The time taken by it to travel from the extreme position to half the amplitude is :
A $\frac{T}{6}$
B $\frac{T}{4}$
C $\frac{T}{3}$
D $\frac{T}{2}$
A particle performs simple hormonic motion with a period of 2 seconds. The time taken by it to cover a displacement equal to half of its amplitude from the mea n position is
A $1 / 2$ s
B $1 / 3$ s
C $1 / 4$ s
D $1 / 6$ s