A disc is rolling (without slipping) on a horizontal surface. C is its center and Q and P are two points equidistant from C. Let VP,VQ and VC be the magnitude of velocities of points P,Q and C respectively, then
 .
.
vQ>vC>vP
vQ<vC<vP
vQ=vP, vC=vP
vQ<vC>vP
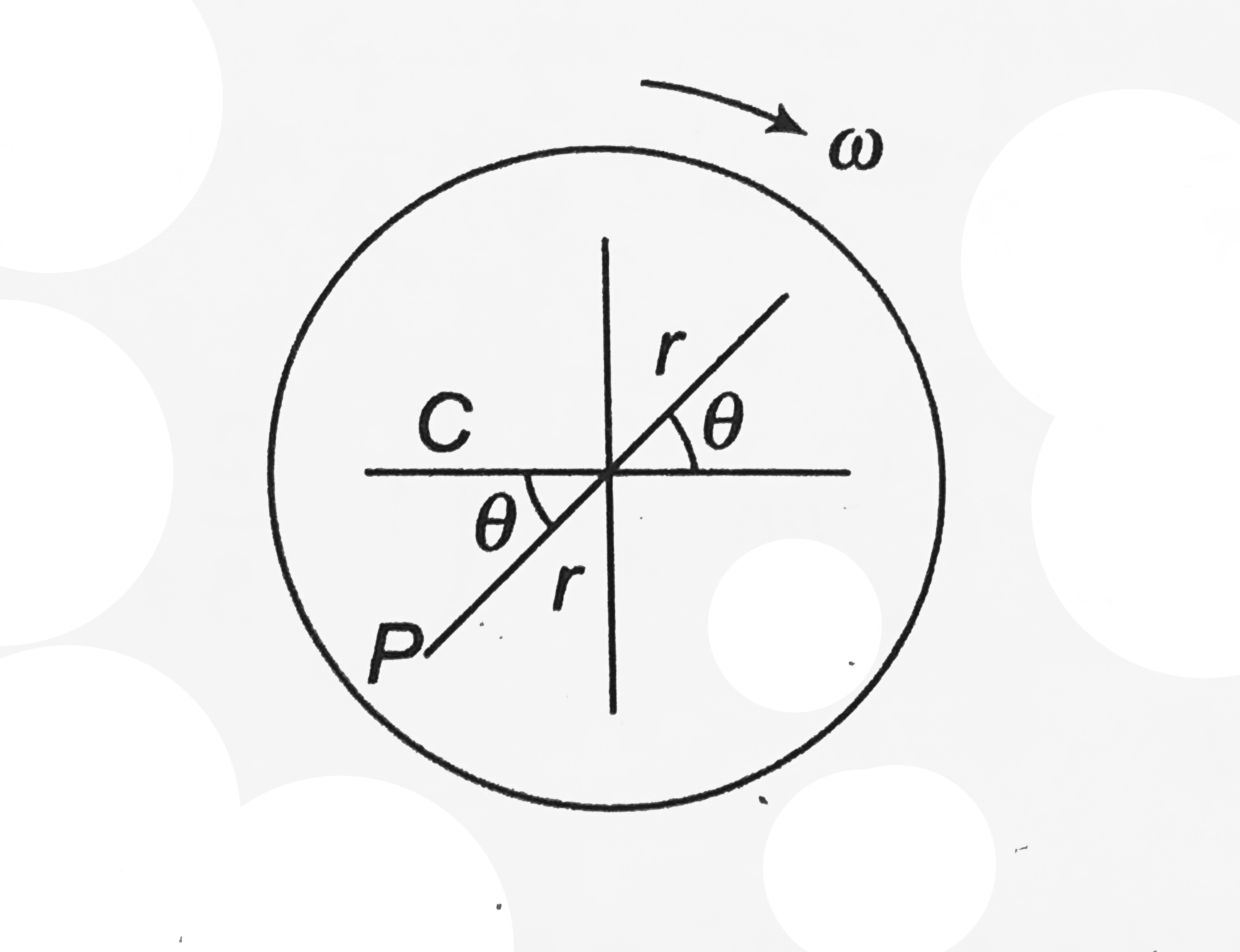
vC=v
P: 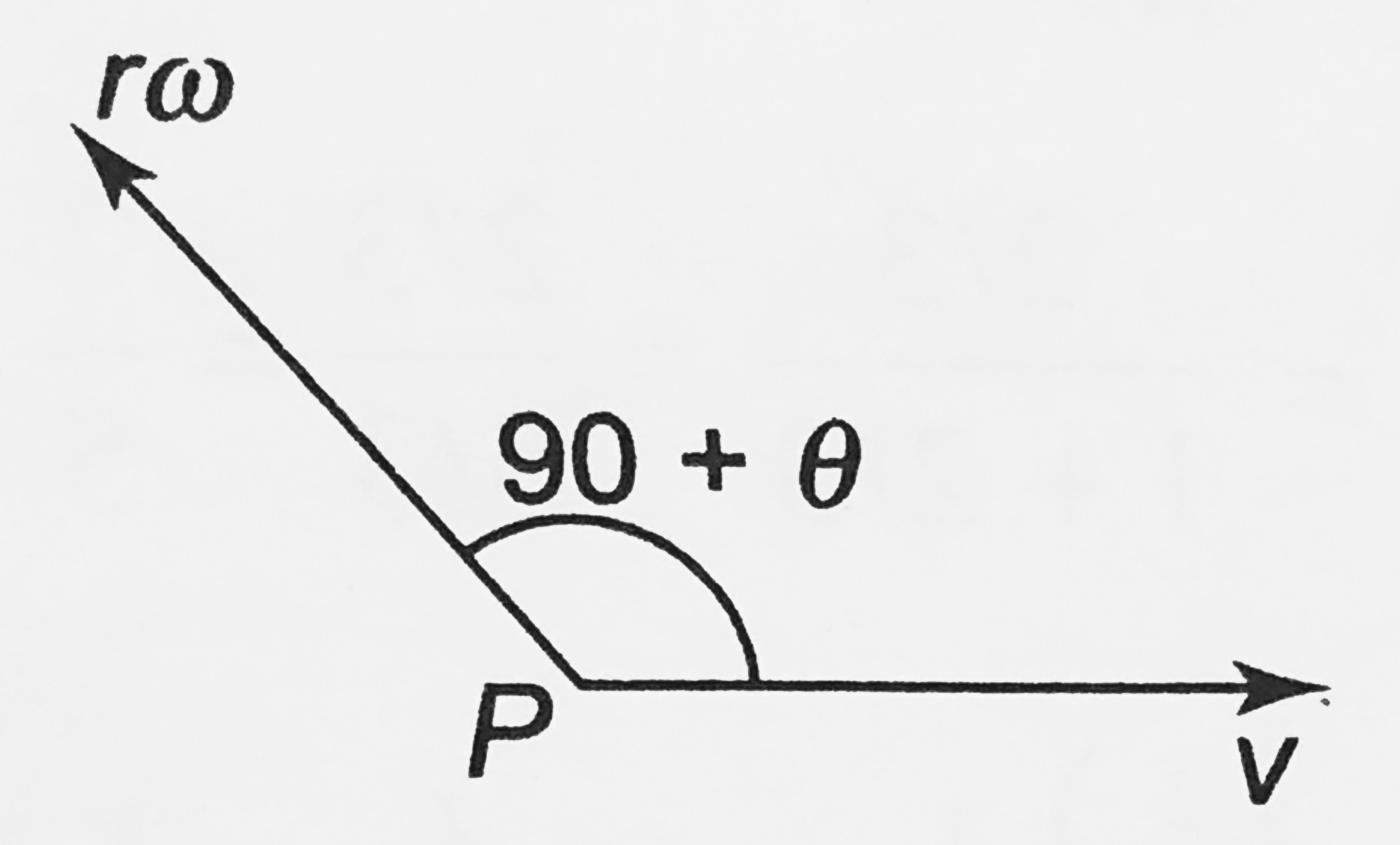
vP=√v2+(rω)2+2×v×rωcos(90+θ)
Q: 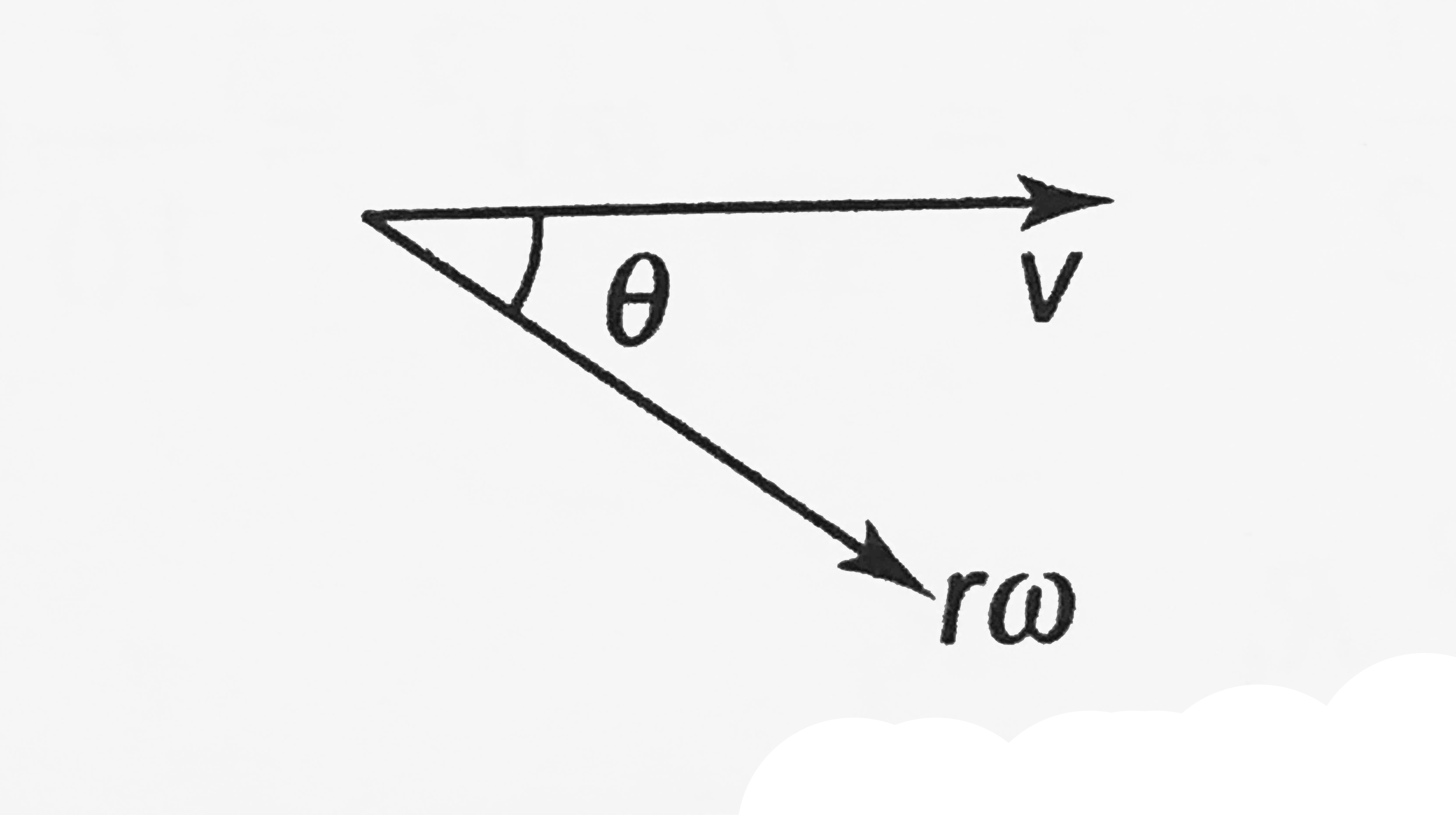
vQ=√v2+(rω)2+2×v×rωcosθ
vQ>vC>vP
OR
Assuming motion as the case of pure rotation about the point of contact 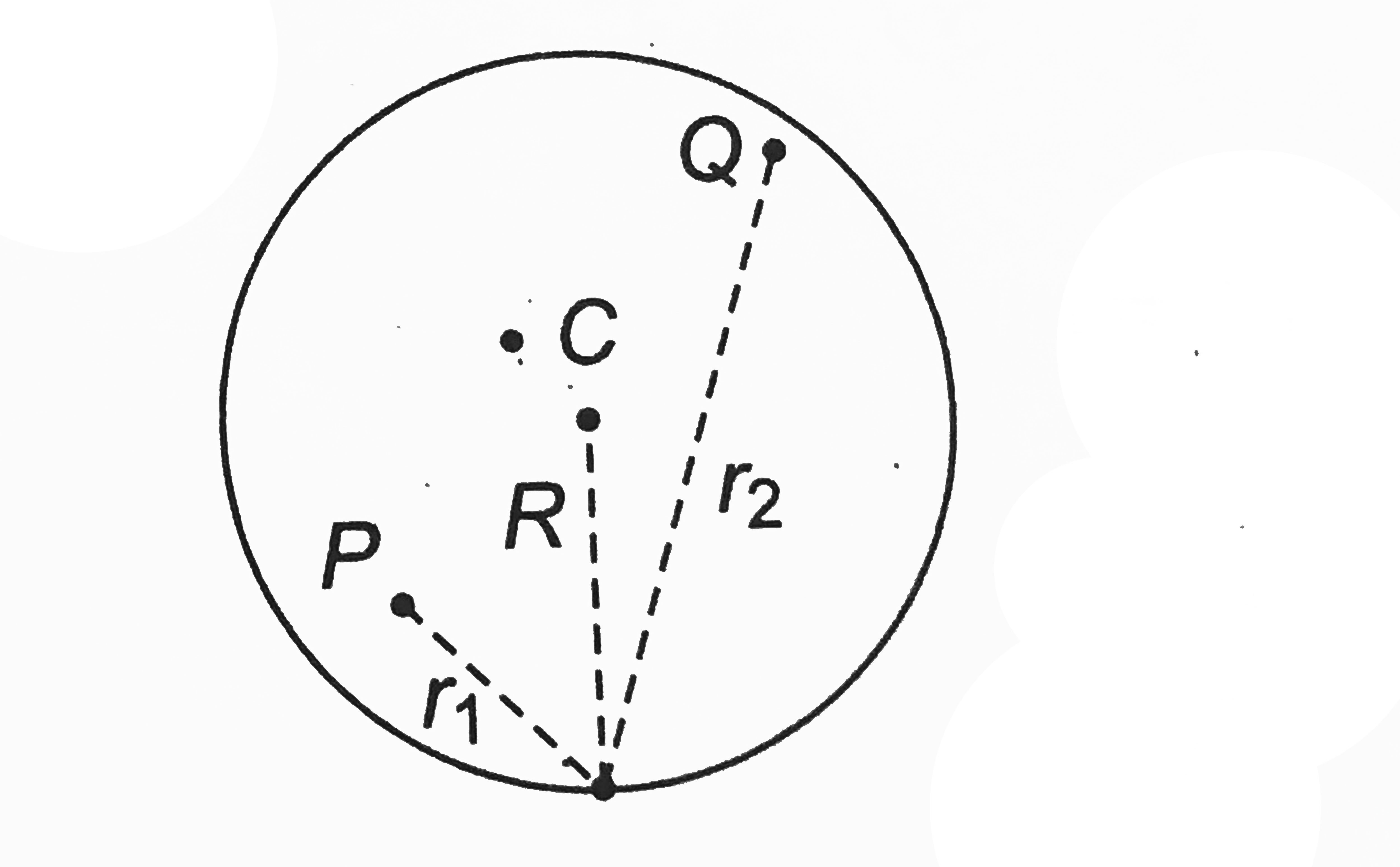
vC=Rω,vQ=r2ω,vP=r1ω
vQ>vC>vP
Topper's Solved these Questions
Similar Questions

A disc is rolling (without slipping) on a horizontal surface. C is its centre and Q and P are two point equidistanec from C. let υp,υQ and υC be the magnitude of velocities of points P, Q, and C repsectively,
(a). υQ>υC>υP
(b). υQ<υC<υP
(c). υQ=υP,υC=12υP
(d). υQ<υC>υP
View SolutionA disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
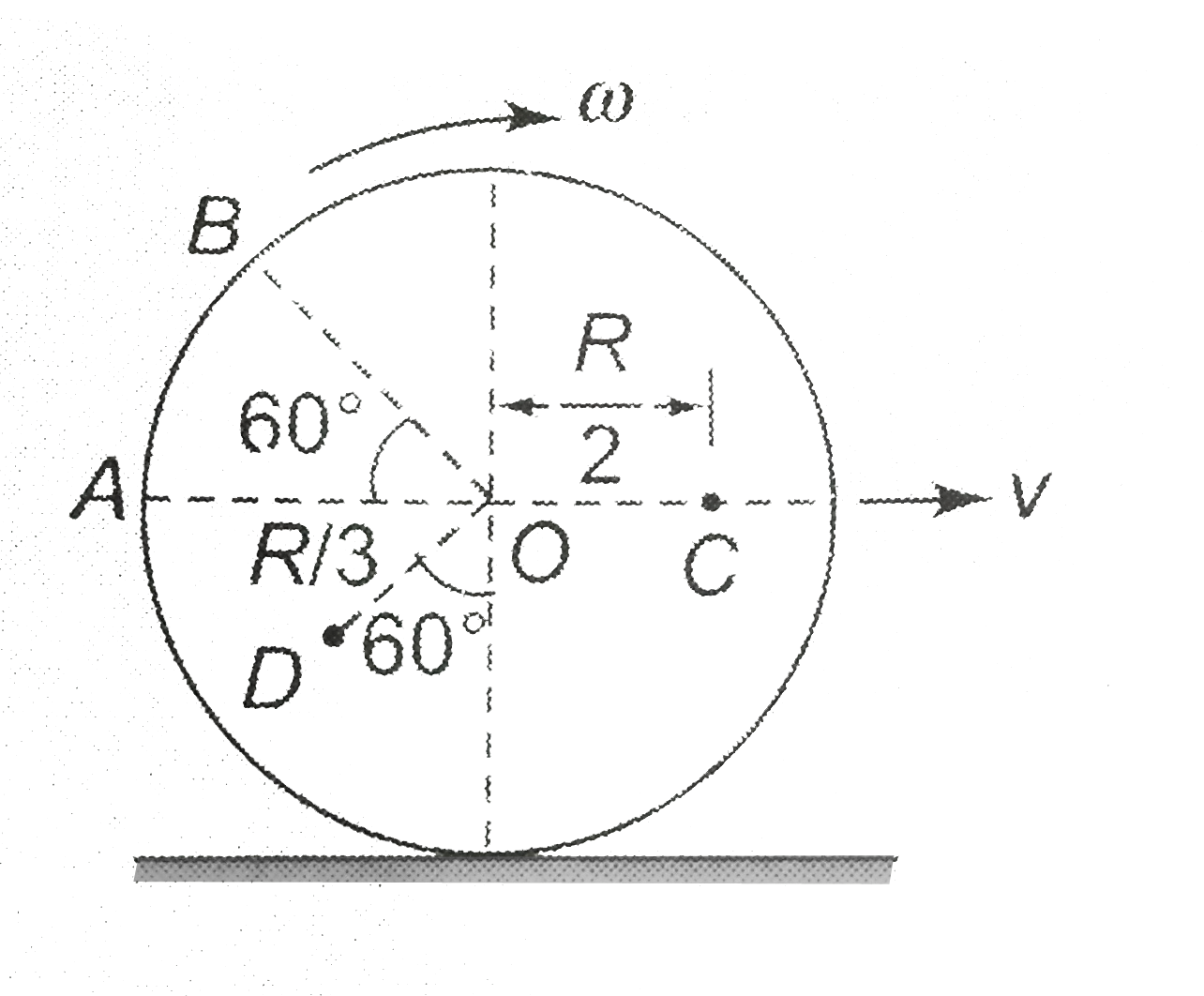
View Solution
Knowledge Check
A disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let vP,vQandvC be the magnitudes of velocities of point P,Q and C respectively, then
 AvQ>vC>vPBvQ<vC<vPCvQ=vP,vC=12vPDvQ<vC>vP
AvQ>vC>vPBvQ<vC<vPCvQ=vP,vC=12vPDvQ<vC>vPA disc is rolling without slipping with angular velocity ω. P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is
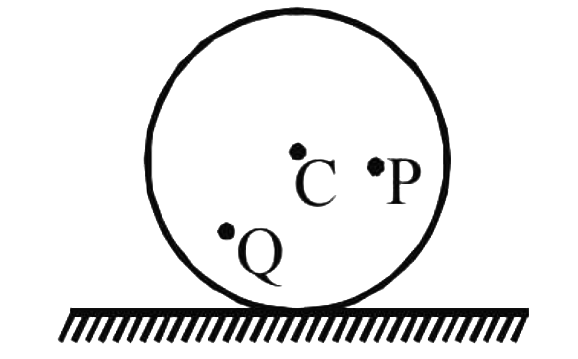 AvQ>vC>vPBvP>vC>vQCvP=vC,vQ=vC2DvP<vC>vQ
AvQ>vC>vPBvP>vC>vQCvP=vC,vQ=vC2DvP<vC>vQA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.
 AVB2VC3VD2V3
AVB2VC3VD2V3
The point P(x,y) is equidistant from the points Q(c+d,d−c)andR(c−d,c+d) then
View SolutionA hollow conducting sphere is placed in an electric field produced by a point charge placed at P as shown in figure.
Let VA,VB,VC be the potentials at points A,BandC respectively. Then
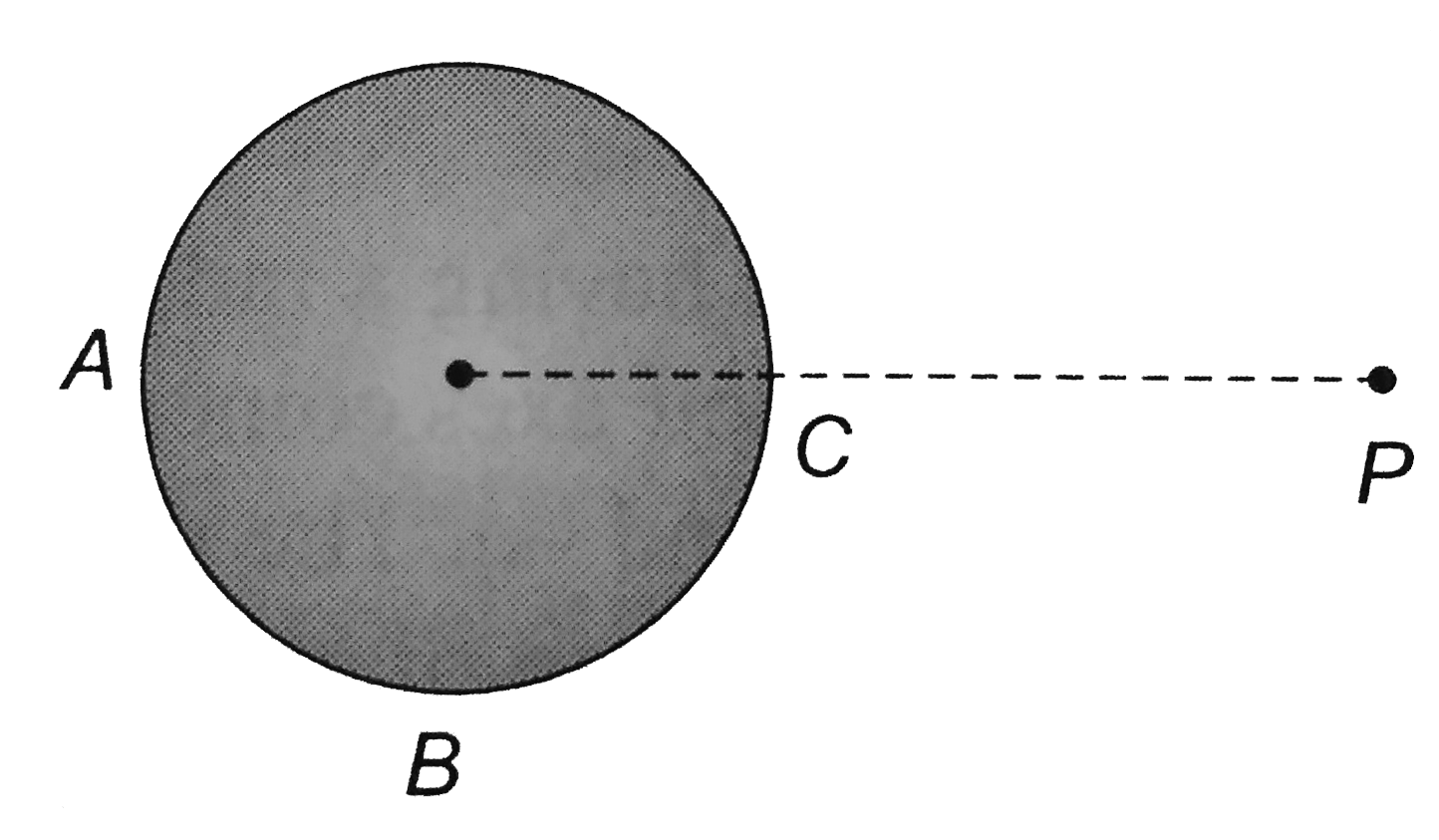
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View SolutionA solid disc rolls clockwise without slipping over a horizontal path with a constant speed v. Then the magnitude of the velocities of points A,B and C (see figure) with respect to a standing observer are, respectively,
 .
.
View Solution

