A rod of length L, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
√2gL
√2gL
√3gL
√3gL
The correct Answer is:C
To find the linear velocity of the top of the rod when it hits the floor, we can use the principles of rotational motion and energy conservation. Here’s a step-by-step solution:
Step 1: Understand the System
The rod is hinged at the bottom and falls under the influence of gravity. When it falls, it rotates about the hinge point at the bottom.
Step 2: Identify the Initial and Final States
- Initial State: The rod is vertical and at rest. The potential energy is maximum, and kinetic energy is zero.
- Final State: The rod is horizontal just before it hits the floor. The potential energy is zero, and kinetic energy is at its maximum.
Step 3: Calculate the Initial Potential Energy
The center of mass of the rod is located at a distance of L2 from the hinge. The initial height of the center of mass is L2, so the initial potential energy (PE_initial) is given by:
PEinitial=mgh=mg(L2)
where m is the mass of the rod and g is the acceleration due to gravity.
Step 4: Calculate the Final Kinetic Energy
When the rod is horizontal, all the potential energy has converted into kinetic energy. The kinetic energy (KE) of the rod can be expressed as:
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge and ω is the angular velocity.
For a rod rotating about one end, the moment of inertia I is:
I=13mL2
Step 5: Relate Angular Velocity to Linear Velocity
The linear velocity v of the top of the rod is related to the angular velocity ω by:
v=ωL
Step 6: Apply Conservation of Energy
Setting the initial potential energy equal to the final kinetic energy:
mg(L2)=12(13mL2)ω2
Step 7: Simplify and Solve for Angular Velocity
Cancelling m from both sides and simplifying gives:
g(L2)=16L2ω2
ω2=3gL
Step 8: Find Linear Velocity
Substituting ω back into the equation for linear velocity:
v=ωL=L√3gL=√3gL
Final Answer
The linear velocity of the top of the rod when it hits the floor is:
v=√3gL
---
The rod is hinged at the bottom and falls under the influence of gravity. When it falls, it rotates about the hinge point at the bottom.
- Initial State: The rod is vertical and at rest. The potential energy is maximum, and kinetic energy is zero.
- Final State: The rod is horizontal just before it hits the floor. The potential energy is zero, and kinetic energy is at its maximum.
The center of mass of the rod is located at a distance of L2 from the hinge. The initial height of the center of mass is L2, so the initial potential energy (PE_initial) is given by:
PEinitial=mgh=mg(L2)
where m is the mass of the rod and g is the acceleration due to gravity.
When the rod is horizontal, all the potential energy has converted into kinetic energy. The kinetic energy (KE) of the rod can be expressed as:
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge and ω is the angular velocity.
I=13mL2
The linear velocity v of the top of the rod is related to the angular velocity ω by:
v=ωL
Setting the initial potential energy equal to the final kinetic energy:
mg(L2)=12(13mL2)ω2
Cancelling m from both sides and simplifying gives:
g(L2)=16L2ω2
ω2=3gL
Substituting ω back into the equation for linear velocity:
v=ωL=L√3gL=√3gL
The linear velocity of the top of the rod when it hits the floor is:
v=√3gL
Topper's Solved these Questions
Similar Questions
A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
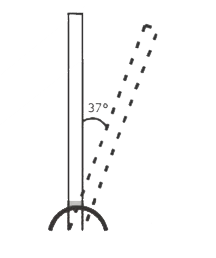
View Solution
Knowledge Check
A meter stick is held vertically with one end on the floor and is allowed to fall. The speed of the other end when it hits the floor assuming that the end at the floor does not slip is (g=9.8m/s2)
A3.2 m/sB5.4 m/sC7.6 m/sD9.2 m/sA meter stick is hold vertically with one end on the floor of the sticks does not move. The velocity of the other end when it hits the floor, will be
A9.8 m/sB6.2 m/sC8.9 m/sD5.4 m/s
A thin meter scale is kept vertical by placing its one end on floor, keeping the end in contact stationary, it is allowed to fall. Calculate the velocity of its upper end when it hit the floor.
View SolutionA metre stick is held vertically with one end on the floor and is then allowed to fall . Find the speed of the other end when it hits the floor , assuming that the end of the floor does not slip . Take g = 10 m/s2.
[√30m/s]
View SolutionA thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionA thin meter scale is kept vertical by placing its lower end hinged on floor. It is allowed to fall. Calculate the velocity of its upper end when it hits the floor.
View SolutionA rod of length L is hinged from one end. It is brought to the horizontal position and released. The angular velocity of the rod when it is in the vertical position is √Kg/L. Then find the value of K.
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View Solution

