A ring, a solid cylinder and a solid sphere, all having same mass and radius, are placed at the top of an incline and released. The friction coefficents between the objects and the incline are same and not sufficient to allow pure rolling.
( $a$ ) Which body will reach the bottom first?
( $b$ ) Which body will have the minimum kinetic energy at the bottom?

Video Solution

Text Solution

Verified by Experts

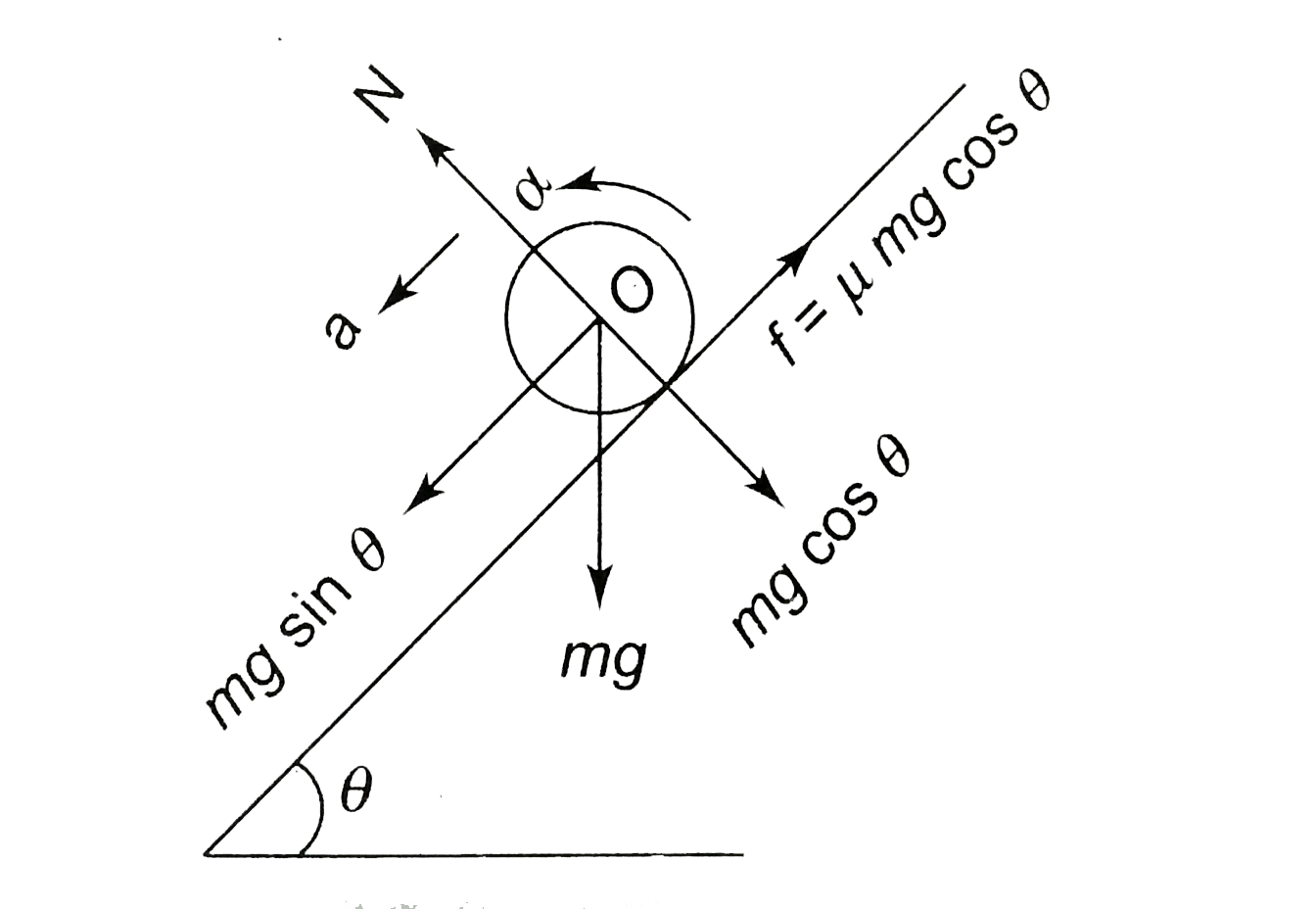
Case of impure rolling, $f = f_{max} = μ m g cos θ$
$m g sin θ - μ m g cos θ = m a$
$a = g sin θ - μ g cos θ$
$s = u t + \frac{1}{2} a t^{2} = 0 + \frac{1}{2} a t^{2}$
$t = \sqrt{\frac{2 s}{a}}$
$v = u + a t = 0 + a t = a t$
(a) Acceleration will be same for all bodies, hence they will reach at the bottom in same time with same linear kinetic energy.
(b) $τ_{0} = f R = I α$
$α = \frac{f R}{I}$
$ω = ω_{0} + a t = 0 + \frac{f R}{I} t$
$K_{R} = \frac{1}{2} I ω^{2} = \frac{1}{2} \times I {(\frac{f R t}{I})}^{2}$
$K_{R} α \frac{1}{I}$
The body with maximum moment of inertia will have minimum rotational kinetic energy at the bottom.
Hence the ring will be with minimum kinetic energy at the bottom.

Updated on:21/07/2023

A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
Athe solid sphere
Bthe hollow sphere
Cthe disc
Dall will achieve same kinetic energy.
A solid sphere a hollow sphere and a disc all having same mass and radius, are placed at the top of a moth incline and released. Least time will be taken in reaching the bottom by
Athe solid sphere
Bthe hollow sphere
Cthe disc
Dall wil take same time
P is a solid sphere and Q is a hollow sphere both having the same mass and radius .If they roll down from the top of an inclined plane , on reaching the bottom .
AVelocity of P is more
BVelocity of Q is more
CVelocity of P = velocity of Q
DNone