A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.

This is the case of impure rolling. As v0>Rω, friction will act in backward direction to the given linear retardation and angular acceleration so that linear velocity decreases and angular velocity increases so that velocity after time t , v equals Rω (case of pure rolling)
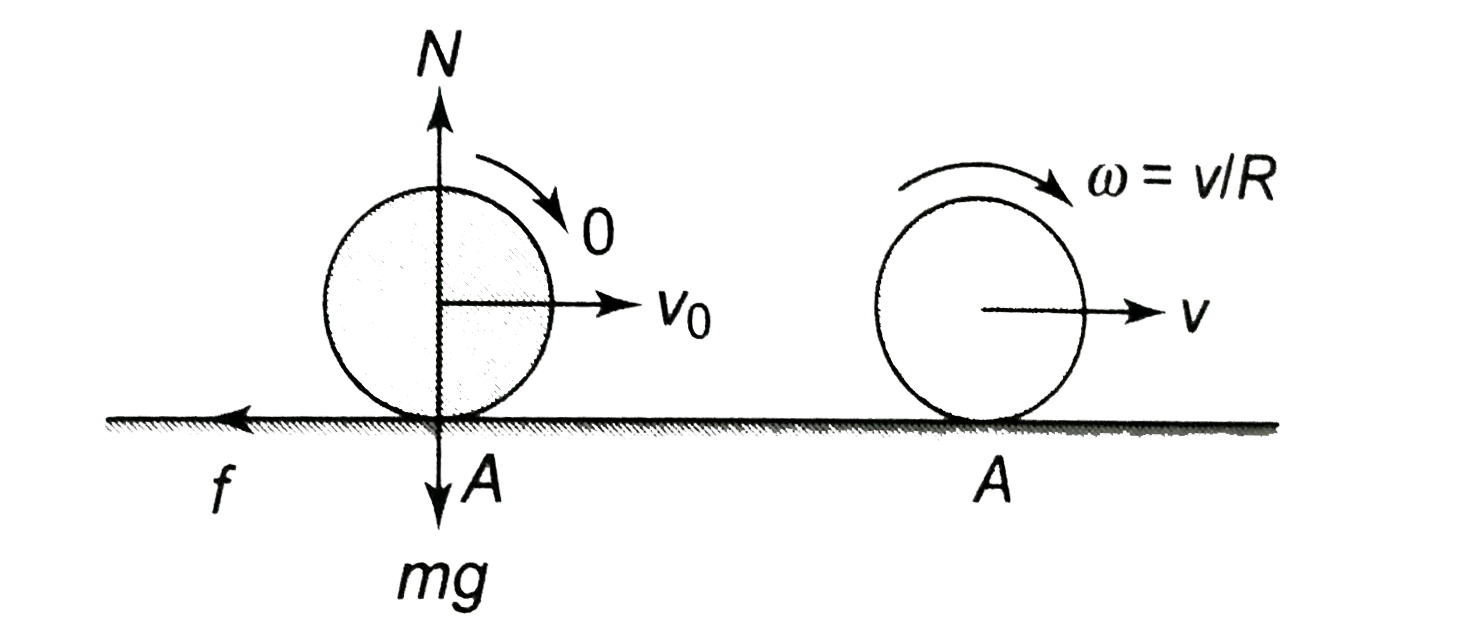
(a) By consevation of angular momentum about A
mv0R=mvR+Ic.m.ω=mvR+12mR2(vR)
=32mvR
v=2v03
(b) In impure rolling, friction is f=fmax=μN=μmg
Retardation a=fm=μmgm=μg
v=v0−at0⇒2v03=v0−μgt0⇒t0=v03μg
After attainment of pure rolling, friction vanishes and the body rolls without slipping forever.
Topper's Solved these Questions
Similar Questions
A uniform disk of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds it acquires a purely rolling motion as shown in figure.
(i) Calculate the velocity of the centre of mass of the disk at t0.

(ii) Assuming the coefficient of friction to be μ calculate t0. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t much longer than t0.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View Solution
Knowledge Check
A uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
A−μmgdB−14mv20CμmgdD−18mv20
A disc of mass M and radius R is rolling purely with centre's velcity v0 on a flat horizontal floor when it hits a step in the floor of height R/4 The corner of the step is sufficiently rough to prevent any slippoing of the disc against itself. What is the velocity of the centre of the disc just after impact?A4v0/5B4v0/7C5v0/6Dnone of theseA uniform disc is having a pure rolling motion on a moving plank as shown in the figure. Choose the correct option among the following .
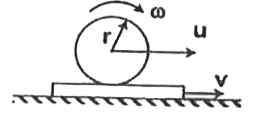 Au−rω=−vBu−rω−v=0C−u=rω+vDnone of above
Au−rω=−vBu−rω−v=0C−u=rω+vDnone of above
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then

View SolutionA cylinder is rotating with angular velocity ω0 and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
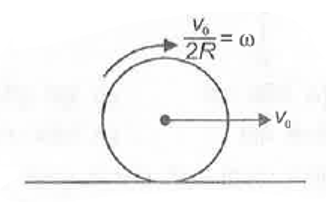
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View Solution
