A uniform cylinder of mass m and radius R starts descending at a moment t=0 due to gravity, Neglecting the mass of the thread, find
(a) the tension of each thread and the angular acceleration of the cylinder,
(b) the time dependence of the instantaneous power developed by the gravitational force.

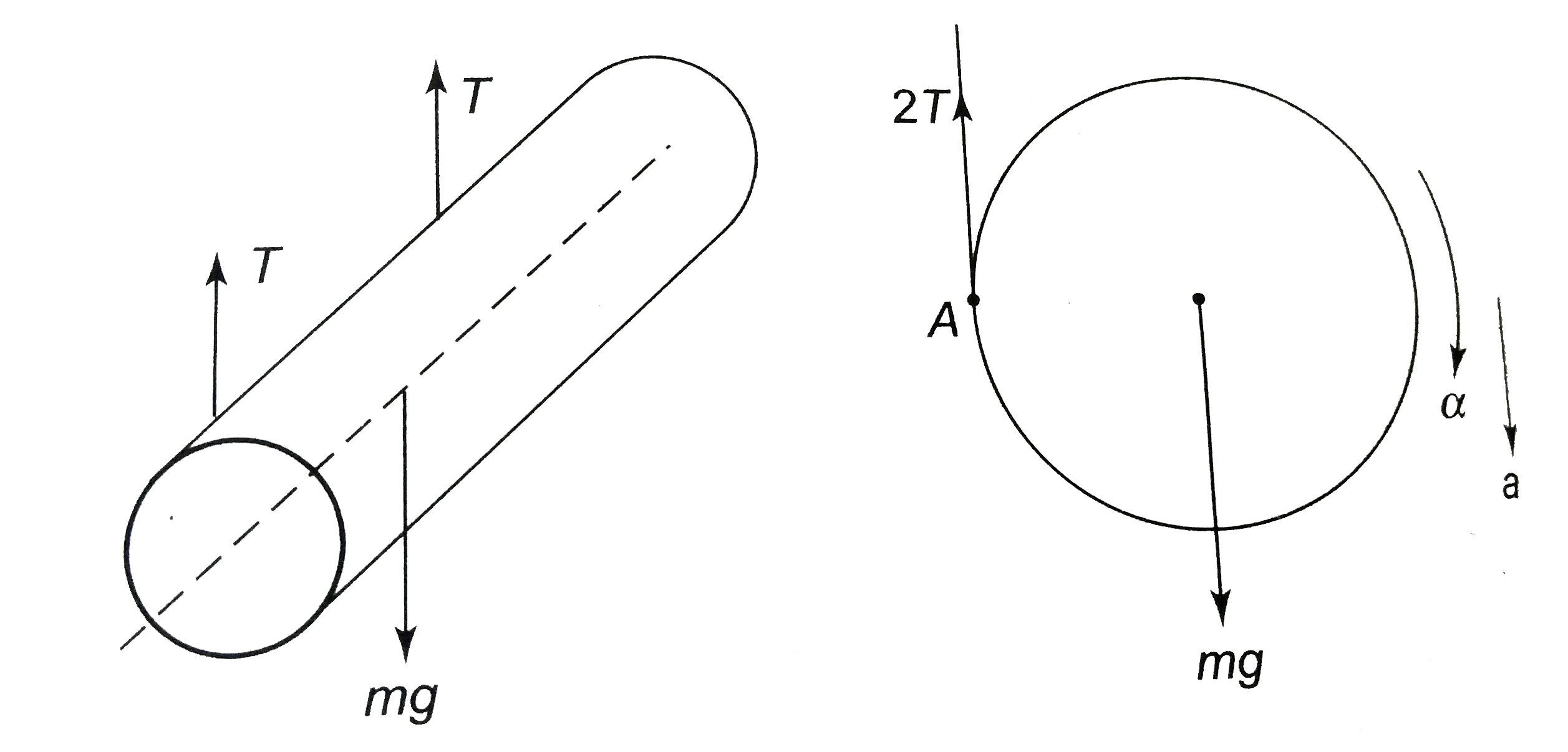
Linear motion: mg−2T=ma (i)
Rotational motion: 2T⋅R=Ic.m.α=12mR2α (ii)
a=Rα (iii)
From (ii), T=14mRα=14ma⇒ma=4T in (i)
mg−2T=4T⇒T=mg6
T=14mRα⇒mg6=14mRα⇒2g3R
a=Rα=2g3
Linear velocity of cylinder after time t
v=at=2gt3
Power delivered by gravitational force
P=m→g⋅→v=mgv=2mg2t3
Tension=mg6
Angular acceleration =2g3R
Power =2mg2t3
OR
Here the cylinder rolls without slipping on vertical surface
a=gsinθ1+k2R2=gsin90∘1+12=23g
Topper's Solved these Questions
Similar Questions
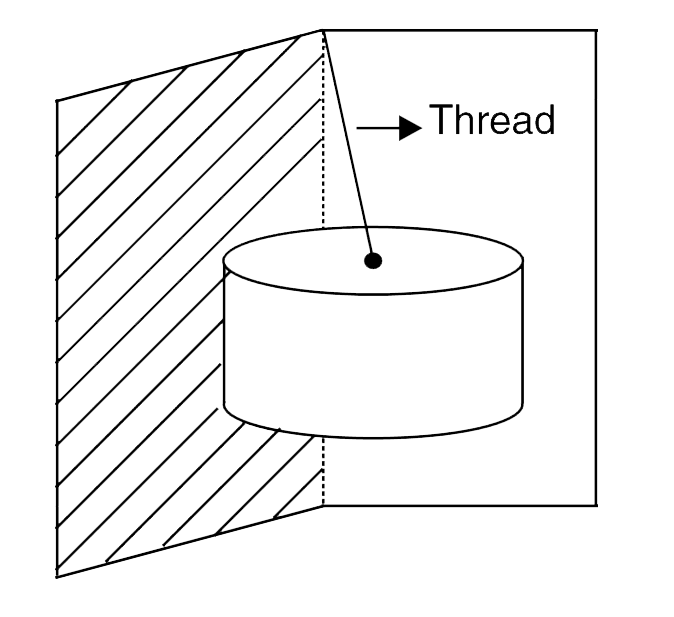
A cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View SolutionA cylinder of mass 0.6kg and radius R is falling under gravity without slipping as the thread is unfolding.Find the tension in the thread (in newton).
View Solution
Knowledge Check
A homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
A2F3MrB3F2MrCF3MrDF2Mr
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3mA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
AMRFBMRFCRMFDFMR
A cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravity
View SolutionA light thread with a body of mass m tied to its end is wound on a uniform solid cylinder of mass M and radius R. At a moment t=0 the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( M=2m).

View SolutionA uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m0 is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

View Solution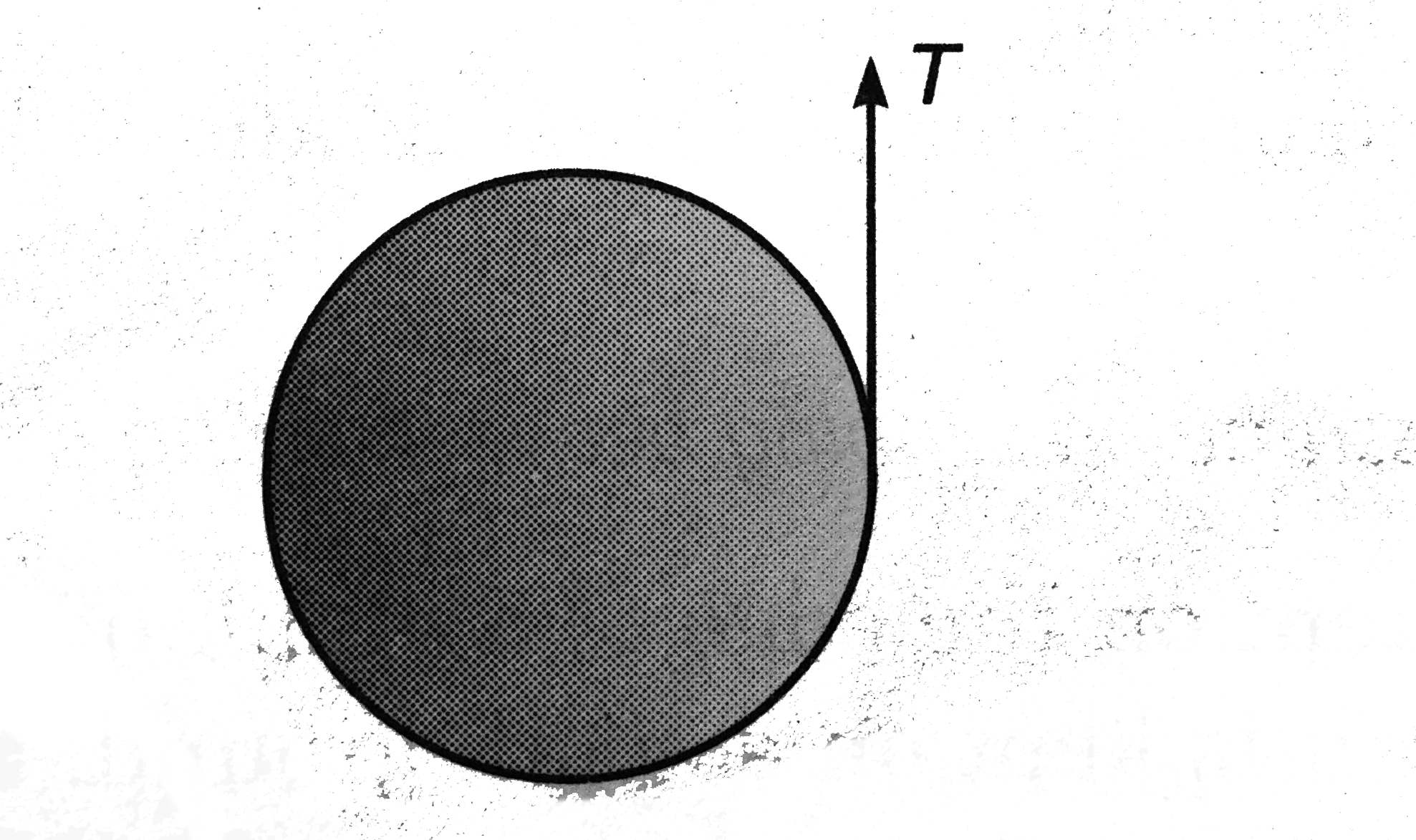
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
View Solution

