A solid sphere of mass m and radius R is hit by a cue at height h above the center of sphere. The cue applies a force F and the contact period is small time t. Find
(a) the velocity of center of mass,
(b) the angular speed of sphere about the center of mass and
(c) the value of h so that the sphere rolls without slipping after removal of force.

Linear impulse
Ft=Δp=m(vc.m.−0)⇒vc.m.=Ftm
Angular impulse about O
τt=ΔL
Fht=Ic.m.(ω−0)
Fht=25mR2ω⇒ω=5Fht2mR
For pur rolling.
vc.m=Rω⇒h=2R5
Topper's Solved these Questions
Similar Questions
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
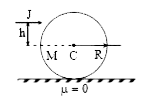 Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JMA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
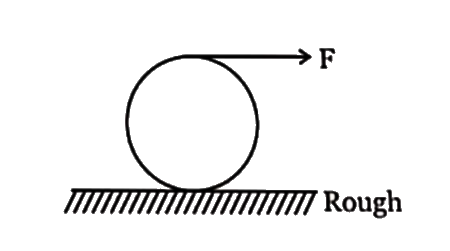
View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)

View Solution
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
View Solution

