A hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).

Conservation of linear momentum
mv=(M+m)vc.m.⇒vc.m.=mvM+m
Conservation of angular momentum about O
mvh=I0ω=(23MR2+mR2)ω
⇒ω=mvh(23M+m)R2
For pure rolling
vc.m.=Rω
mvM+m=mvh(23M+m)R
h=(23M+m)RM+m=2R3(sincem<<M)
Topper's Solved these Questions
Similar Questions
The sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
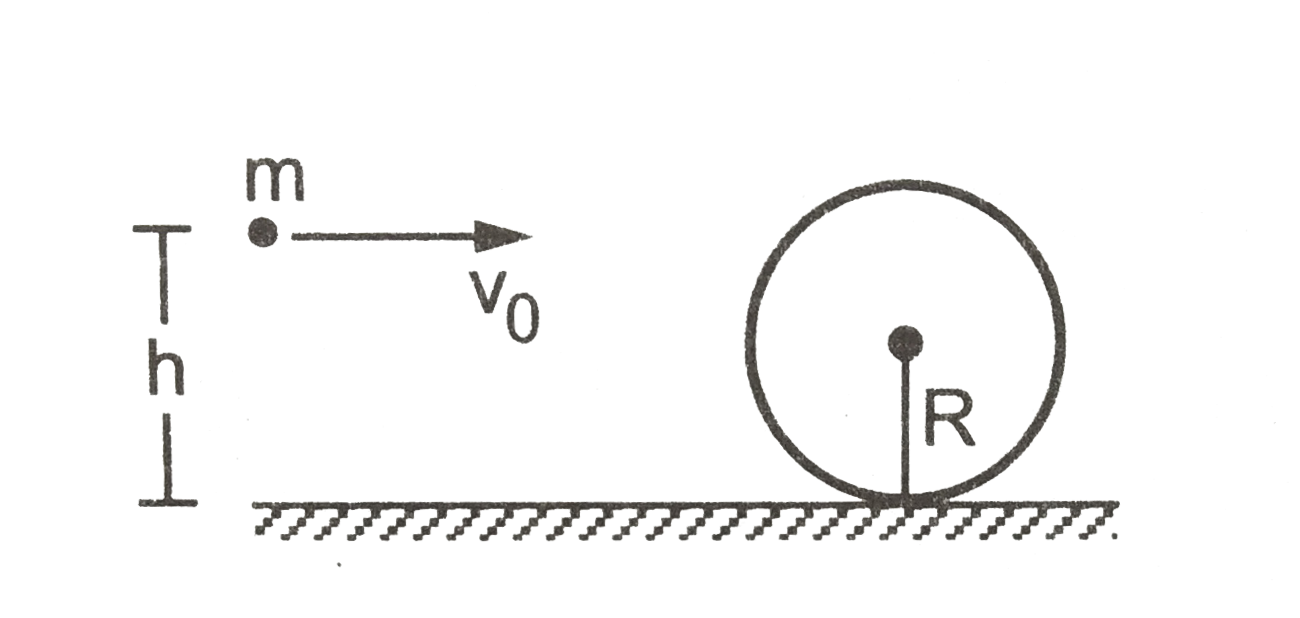
View Solution
A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View Solution
Knowledge Check
Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
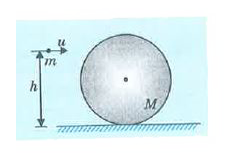
At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.A5R7B3R5C3R7D7R5Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
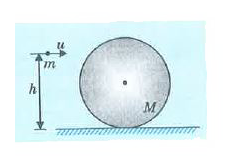
Angular velocity of the sphere just after the collision isA5mu2MRB5mu(h−R)2MR2C2mu(h−R)5MR2D2Mu(h−R)2mR2Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?AmuMBmu2MC2muMDzero
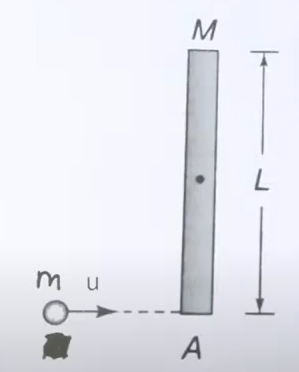
A particle of mass m and speed u collides elastically with the end of a uniform rod of mass M and length L as shown. If the particle comes to rest after collision, find mM
View SolutionA particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collision
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collision
View Solution

