Two metal discs, one with radius r and mass m and the other with radius 2r and mass 2m, are welded together and mounted on a frictionless axis through their common center.
(a) What is the total moment of inertia of the two discs?
(b) A light string is wrapped around the edge of the smaller disc and a block of mass m0 is suspended from the free end of the string. If the block is released from rest at a distance h, what is its speed just before it strikes the floor?

(a) I1=12mr2,I2=12×2m×(2r)2=4mr2
I=I1+I2=9mr22
(b) Loss in the gravitational potential of block = gain in the kinetic energy of (block + disc)
m0gh=12m0v2+12Iω2
v=rω⇒ω=vr
=12m0v2+12×9mr22×v2r2
(12m0+94m)v2=(2m0+9m4)v2
v=√4m0gh9m+2m0
Topper's Solved these Questions
Similar Questions
Two wooden disc , one with radius 2 cm and mass 1 kg and the other with radius 4 cm and mass 2 kg , are welded together coaxially and mounted on a frictionless axis through their common centre. Alight string is wrapped around the edge of the smaller disc, and a 3 kg block is suspended from the free end of the string.What is the acceleration of the block after it is released? Repeat the above process if the stringi swrapped around the edge of the larger disc.
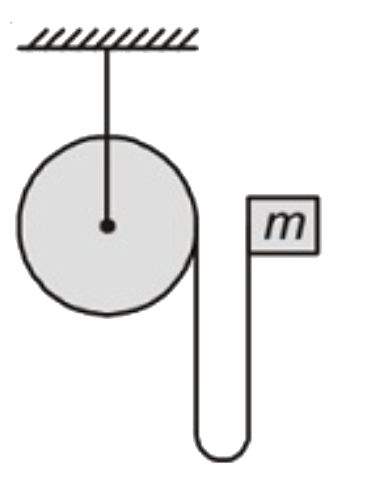
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View Solution
Knowledge Check
From a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A15MR2/32B13MR2/32C11MR2/32D9MR2/32A uniform disc of mass 2 kg and radius 1m is mounted on an axle supported on fixed frictionless bearings. A light chord is wrapped around the rim of the disc and mass of 1kg is tied to the free end. If it is released from rest-
Athe tension in the chord is 5NBin first four seconds the angular displacement of the disc is 40 radCthe work done by the torque on the disc in first four seconds is 200JDthe increase in the kinetic energy of the disc in the first four seconds in 200 JA block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
 A√glR3B√gl2R2C√2gl3R2D√3gl2R2
A√glR3B√gl2R2C√2gl3R2D√3gl2R2
From a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View SolutionFrom a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionFrom a disc of radius R and mass M , a circular hole of diameter R , whose rim passes through the centre is cut . What is the moment of inertia of the remaining part of the disc about a perpendicular axis , passing through the centre ?
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View Solution
