Four identical rods each of mass m and length L are joined to form a square. Find the M.I. about
(a) the x-axis,
(b) the y-axis,
(c) the z-axis,
(d) about 1−1,
(e) an axis passing through one corner and perpendicular to the plane.
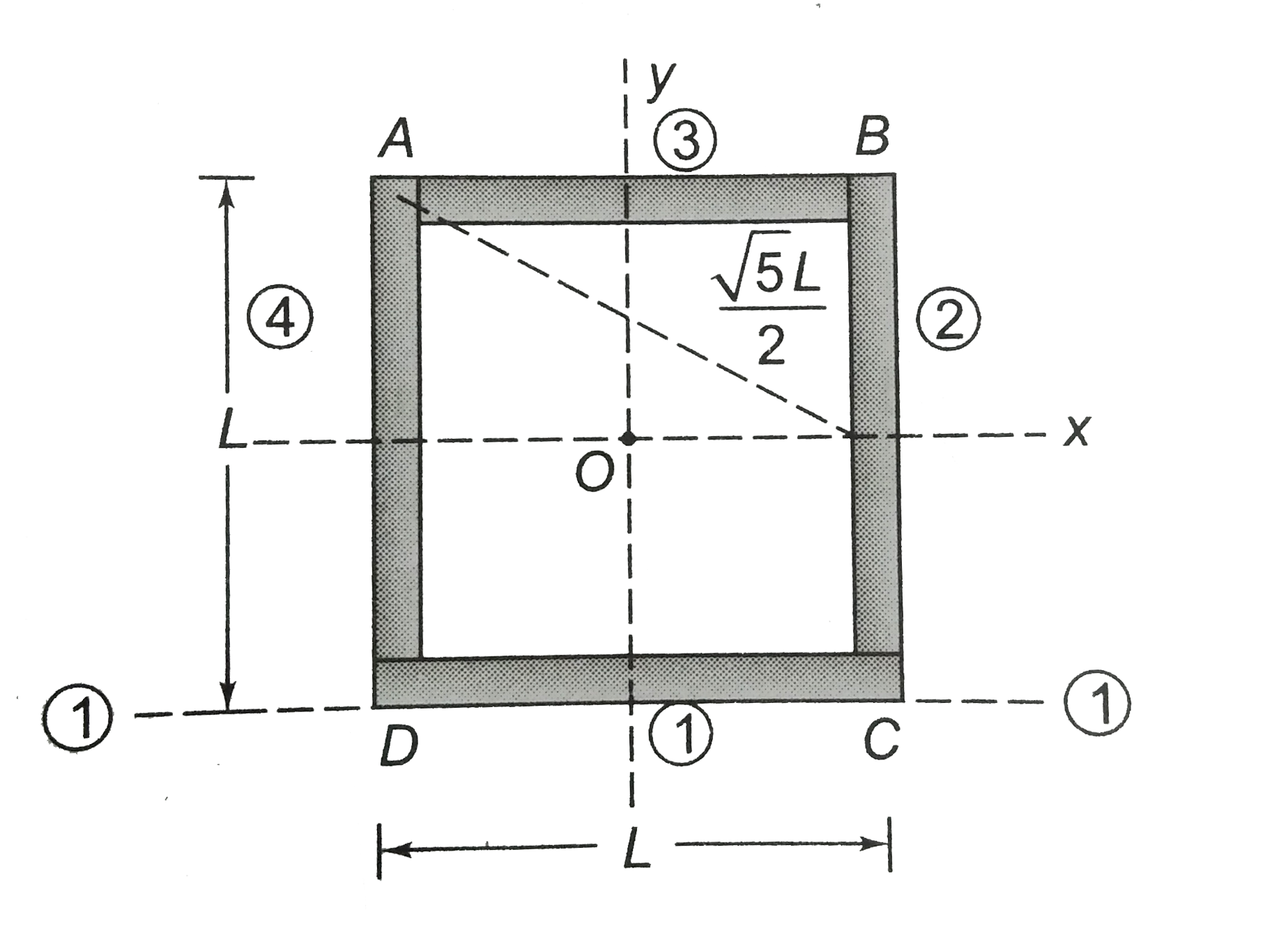
(a) About the x-axis
Rods (2) and (4) each =mL212
Rods (1) and (3) each =[0+m(L2)2]=mL24
Ix=I2+I4+I1+I3
=mL212×2+mL24×23mL2
(b) Iy=Ix=23mL2 (due to symmetry)
(c) Iz=Ix+Iy=4mL22 (⊥ar axes theorem)
(d) I1−1=I1+(I2+I4)+I3
=0+mL23×2+{0+mL2}=53mL2
(e) An axis passing through A and ⊥ar to the plane
IA=(I3+I4)+(I1+I2)
=mL23×2+⎧⎨⎩mL212+m(√5L2)2⎫⎬⎭×2
=103mL2
OR
O is the center of mass system of rods
IA=(Iz)c.m.+4m(L√2)2
=43mL2+2mL2=103mL2
For continuous or Distributed Mass
I=∫r2dm
dm: mass element
r:⊥ar distance of element from axis
Topper's Solved these Questions
Similar Questions

Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
View SolutionThree thin, uniform, indentical rods each or mass M and length L are joined as shown. Find the M.I. about an axis passing through O and perpendicular to the plane.
View Solution
Knowledge Check
Two uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
AMl212BMl26CMl24DML23For identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.
 A53ml2B43ml2Cml2DNone of these
A53ml2B43ml2Cml2DNone of theseTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
Aml2/12Bml2/6Cml2/3Dml2/2
find the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its eneds and perpendicular to its length.
View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
View Solution