Find the M.I.
(a) An axis passing through A and ⊥ar to the length.

(b) (i)An axis passing through the perimeter of ring and ⊥ar to the plane.

(ii) An axis touching the perimeter and lying in the same the plane.
(c) Solid sphere

An axis touching the sphere (tangential axes)
(d) An uniform disc
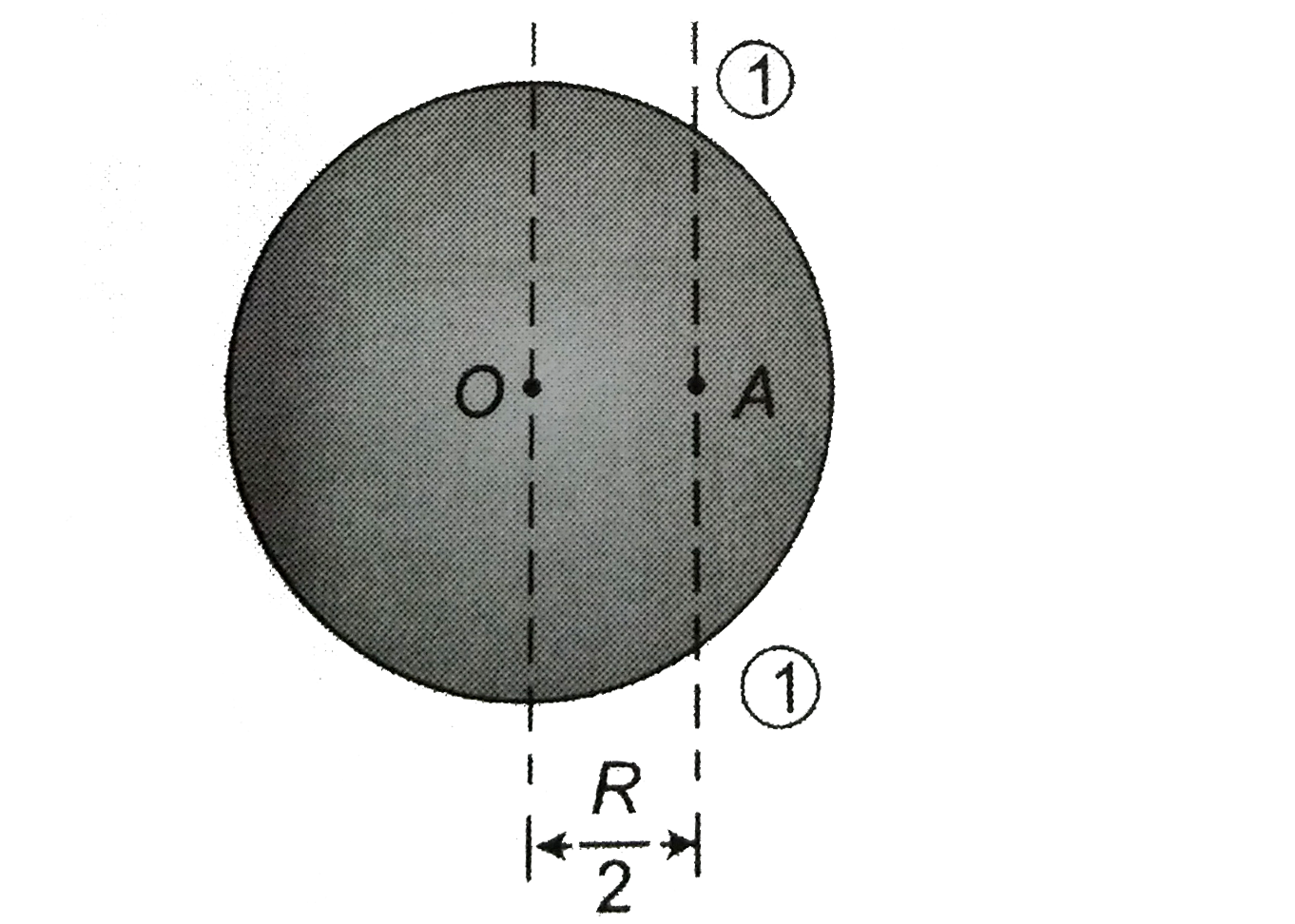
An axis passing through A, parallel to the diameter and lying in the same plane.
Video Solution
Text Solution
These simple problems can be solved with the help of parallel axes theorem. It should be kept in mind that one axis must through the center of mass
(a) 
I1−1=Ic.m+Md2
=ML212+M(L4)2
=ML212+ML216=748ML2
(b) (i) 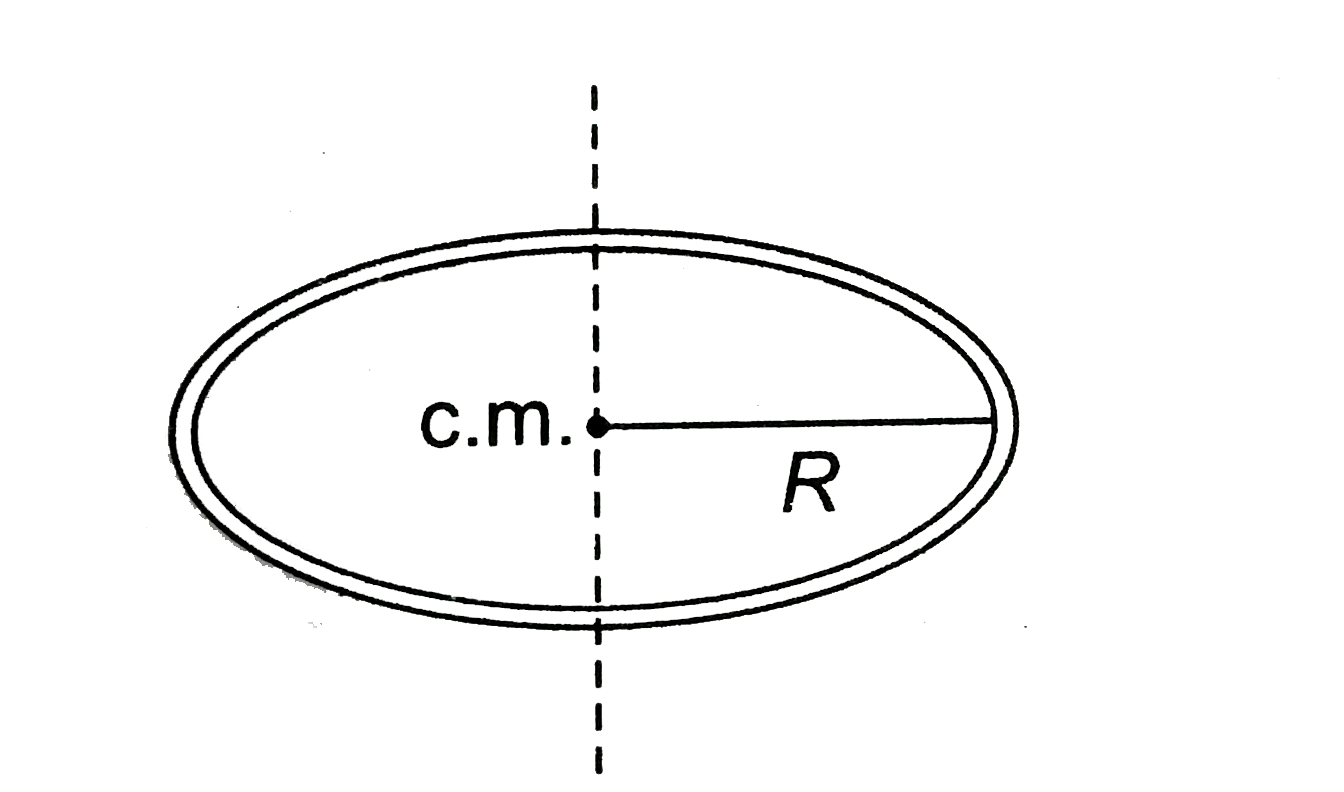
I1−1=Ic.m+Md2=MR2+MR2=2MR2
(ii) 
I1−1=(Ic.m)dia+Md2=12MR2+MR2=32MR2
(c) 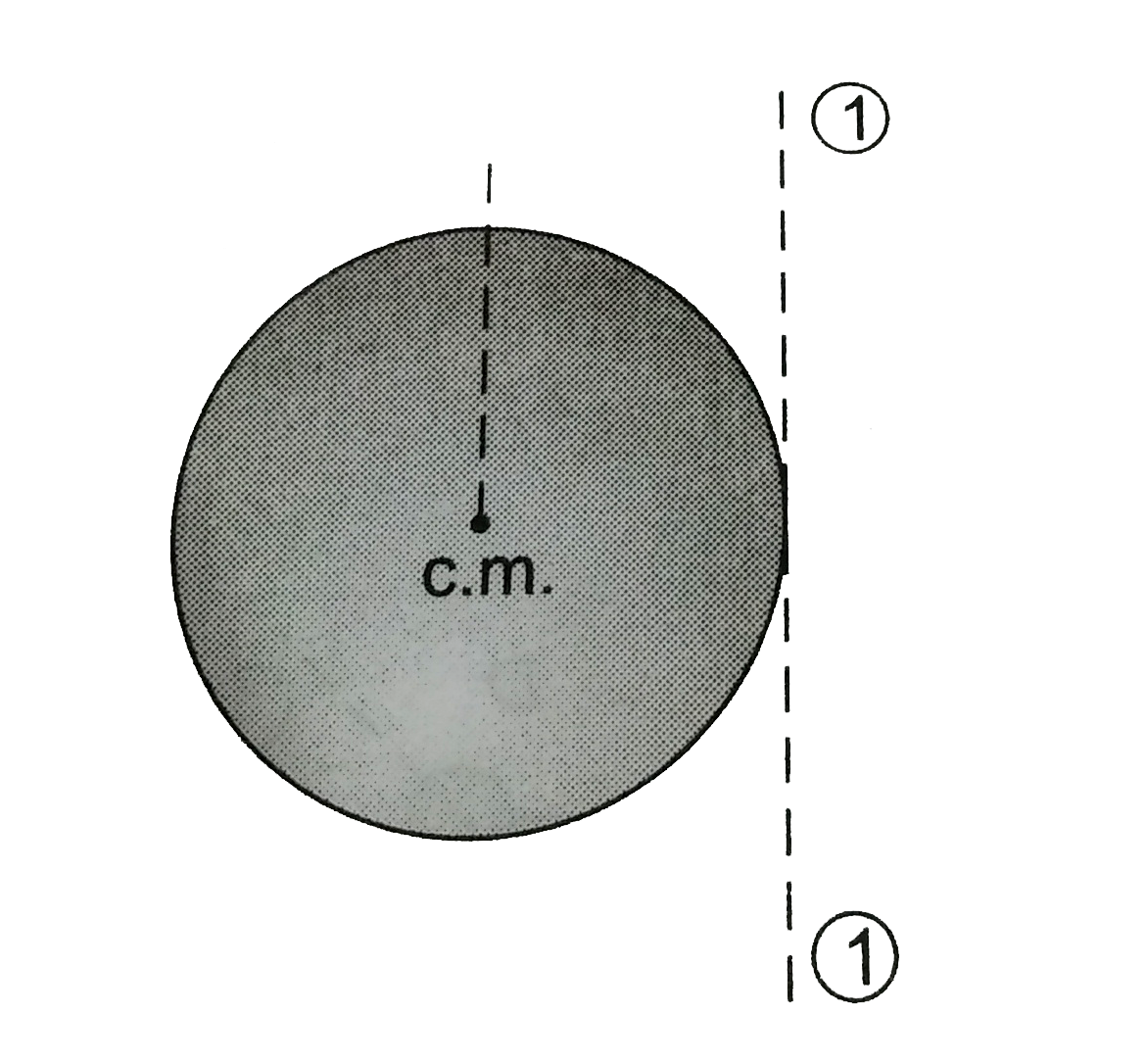
I1−1=Ic.m+Md2=25MR2+MR2=75MR2
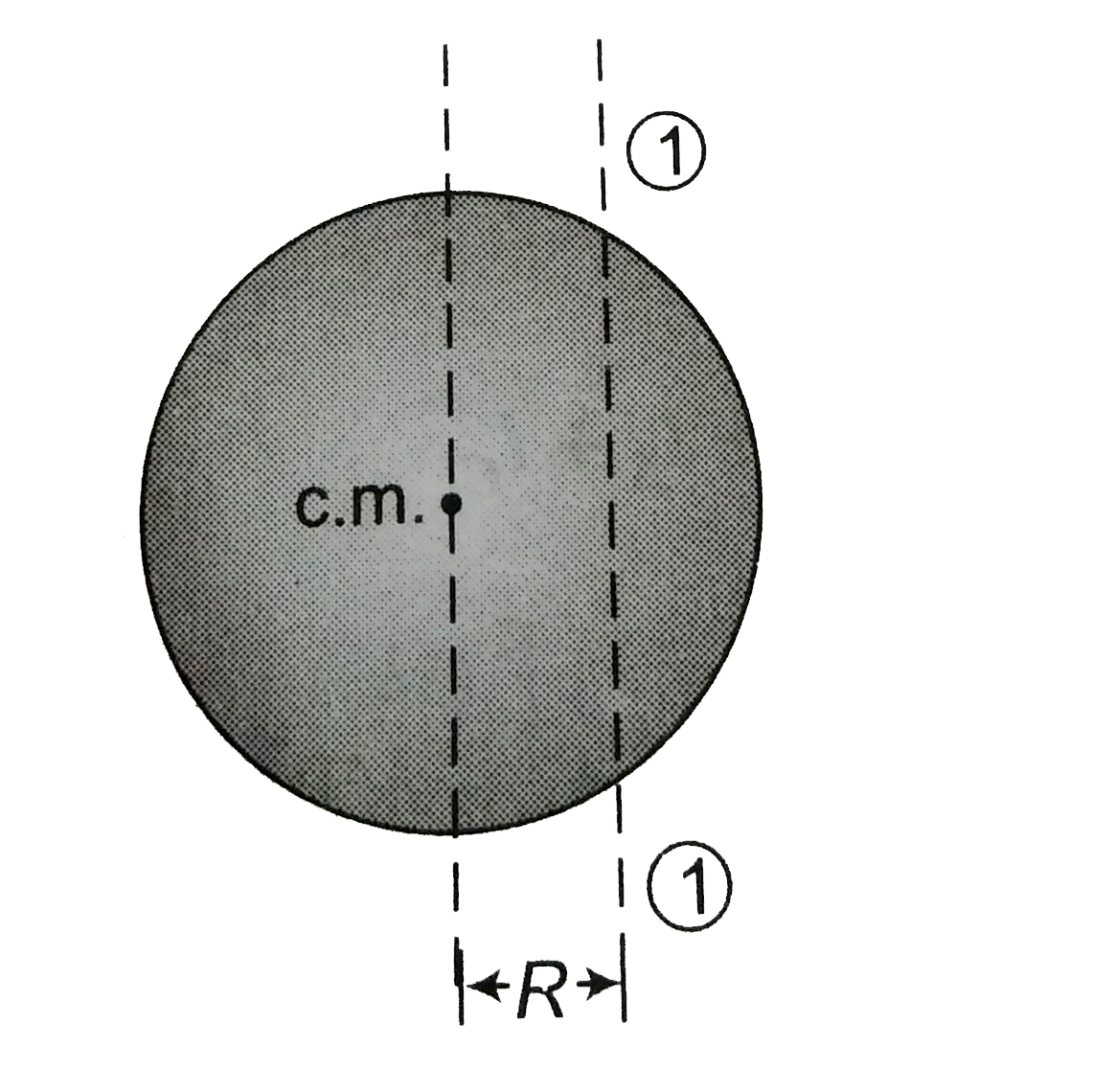
I1−1=(Ic.m)dia+Md2=14MR2+M(R2)2=12MR2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The circle passing through (1, - 2) and touching the axis of x at (3,0) also passes through the point
A(-5, 2)B(2, -5)C(5, -2)D(-2, 5)If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
Amoment of inertia decreasesBmoment of inertia increasesCradius of gyration increasesDradius of gyration decreasesMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Calculate the moment of inertia of a : (a)Disc about an axis passing through its edge and perpendicular to the circular base of the disc. (b) Solid sphere about an axis touching the sphere at its surface?
View SolutionUsing perpendicular axes theorem, find the M.I. of a disc about an axis passing through its diameter.
View SolutionFind the equation of the line which pass through the point (0,0,0) ,and parallel to the following plane: (i) X axis (ii) Y axis (iii) Z axis
View SolutionThe moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
View SolutionA circle touching the X-axis at (3, 0) and making a intercept of length 8 on the Y-axis passes through the point
View Solution