
Consider a situation as shown in the figure. The system is released from rest. When the block of mass m has falled a distance L, its speed becomes √gL3. Find the friction coefficient μ.
When the block of mass m has descended a distance L, distance traveled by the block of mass 2m is 2L. IF the speed of m is v, speed of 2m will be 2v.
Work done against friction =μ×2mg×2L
=4μmgL
Loss in P.E=gain in K.E+work donw against friction
mgL=12mv2+12×2m(2v)2+4μmgL
=92mv2+4μmgL
=92m×gL9+4μmgL
mgL2=4μmgLimpliesμ=18
Topper's Solved these Questions
Similar Questions
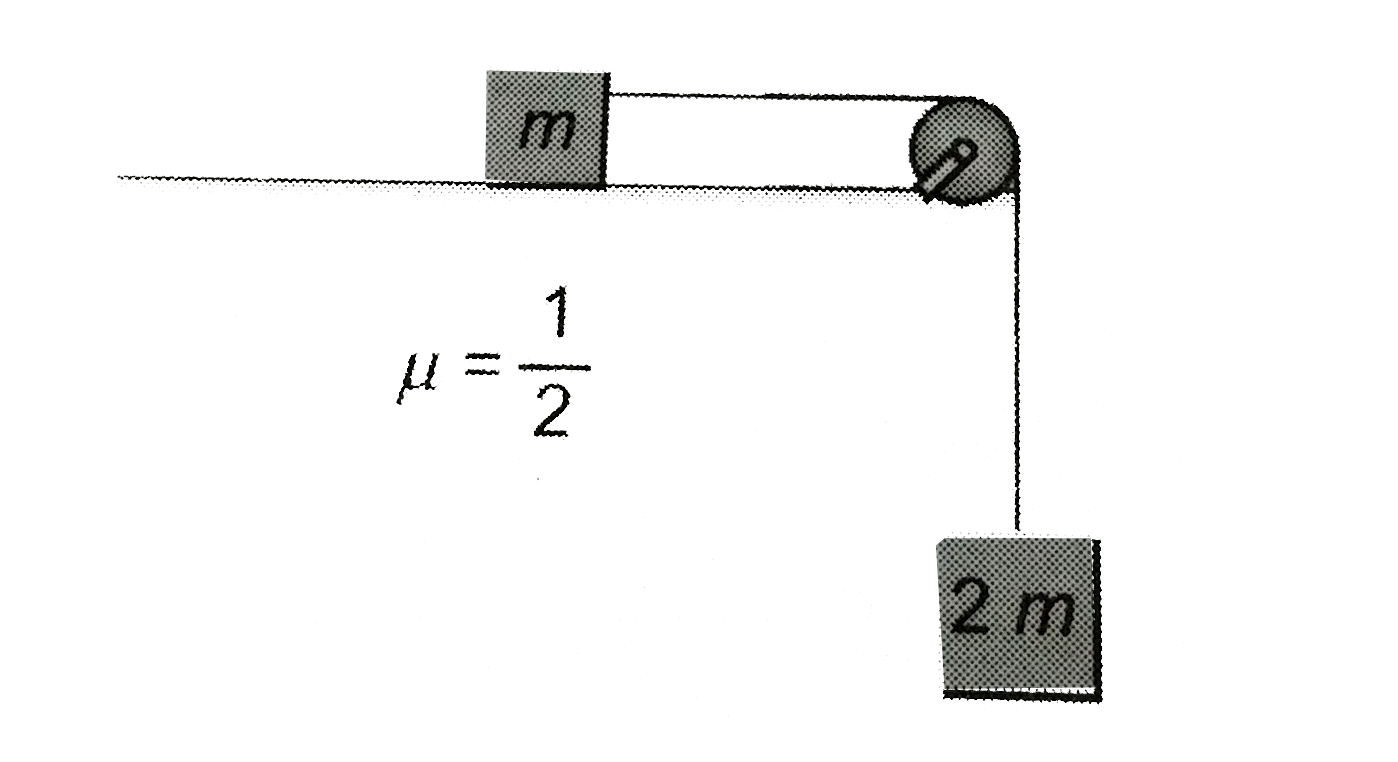
Consider the situation as shown in the figure. The system is released from rest. Find the speed of m when it has traveled a distance d on a rough surface.
View SolutionConsider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
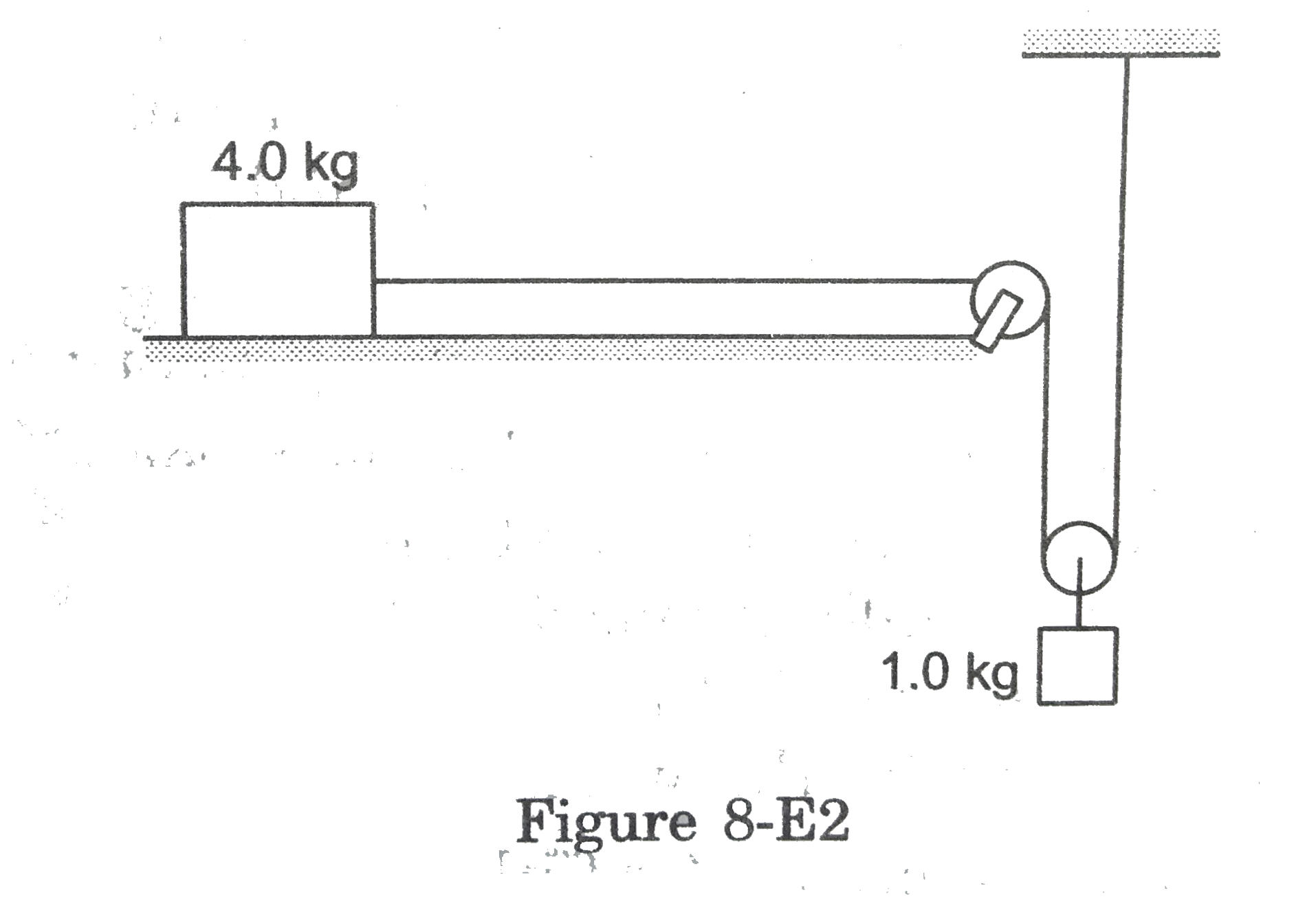
View Solution
Knowledge Check
The system shown in the figure is released from rest. At the instant when mass M has fallen through a distance h, the velocity of m will be
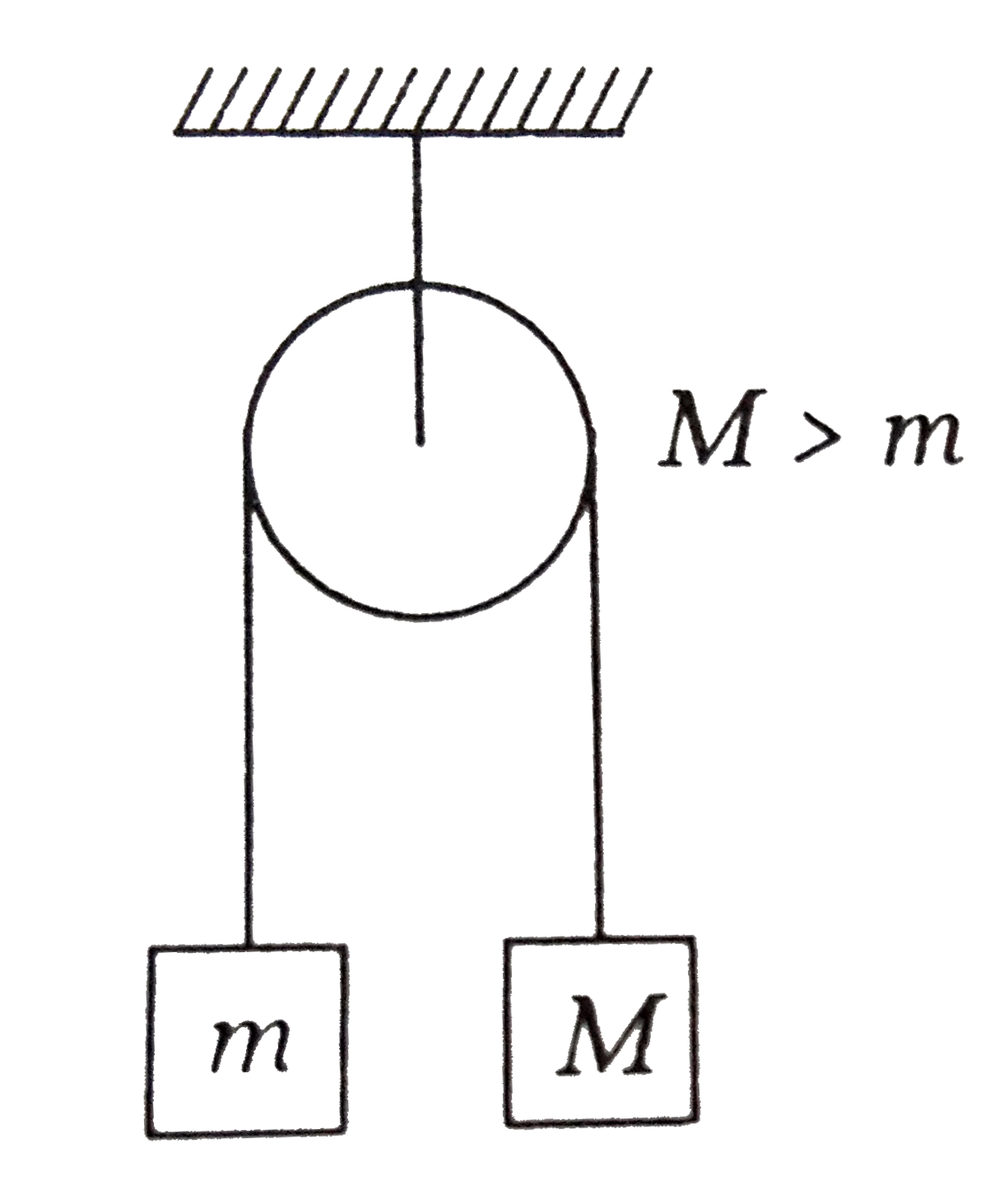 A√2ghB√2ghMmC√2gh(M−m)m+MD√2gh(M+m)m−M
A√2ghB√2ghMmC√2gh(M−m)m+MD√2gh(M+m)m−MThe blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
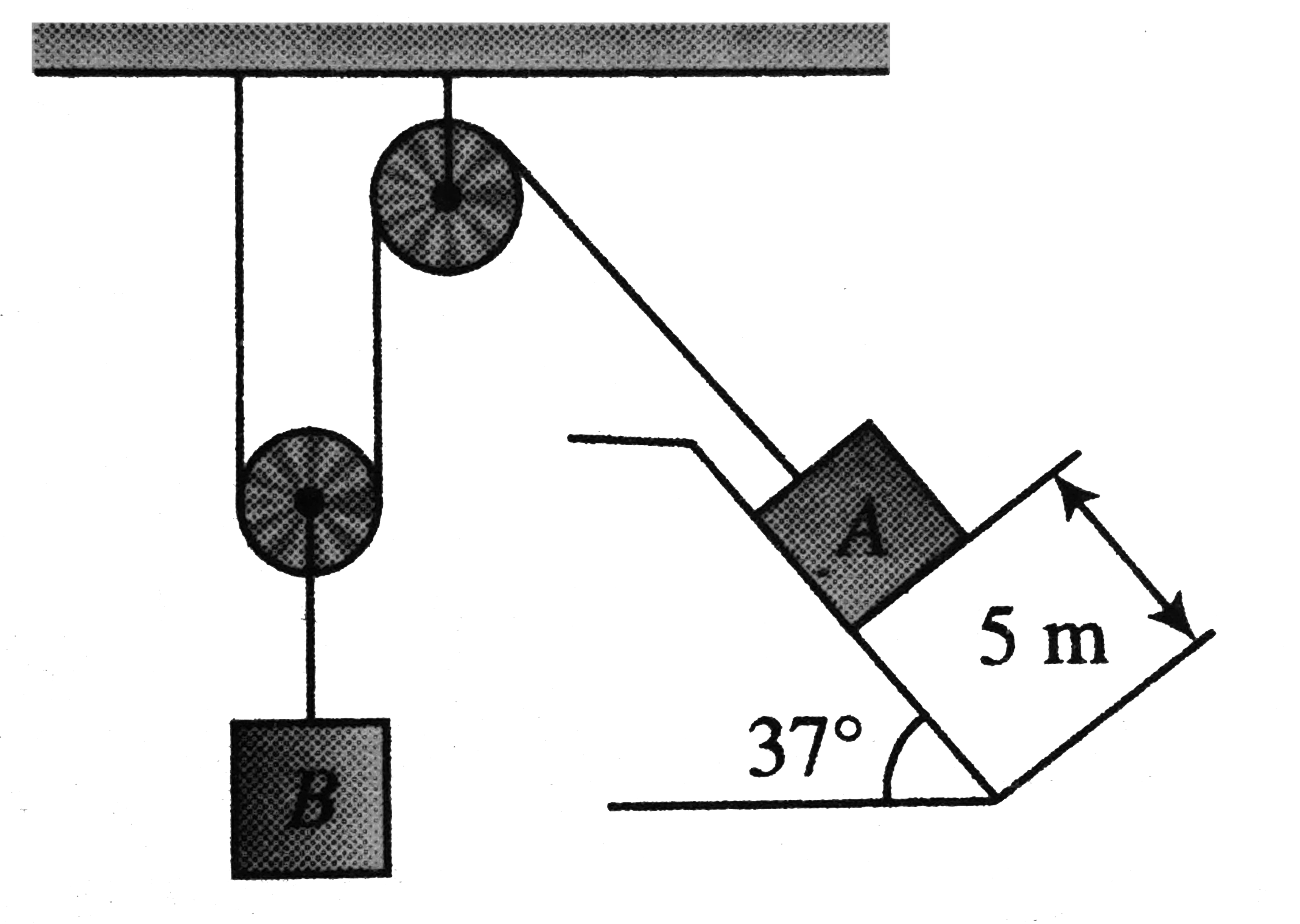 A(a) √32√gB(b) √34√gC(c) √g2√3D(d) √g2
A(a) √32√gB(b) √34√gC(c) √g2√3D(d) √g2
In the figure shown, the system is released frrom rest. Find the velocity of block A when block B has fallen a distance l. Assume all pulleys to be massless and frictionless.

View SolutionConsider the situation as shown in the figgure. The coefficent of friction between the blocks is μ. Find the acceleration of each block.

View SolutionIn the system shown in figure, the block A is released from rest. Find
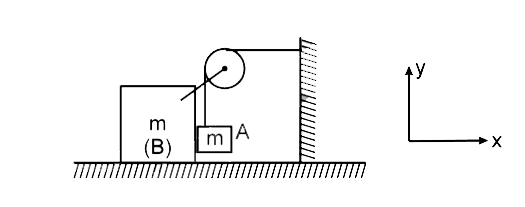
Tension in the string.
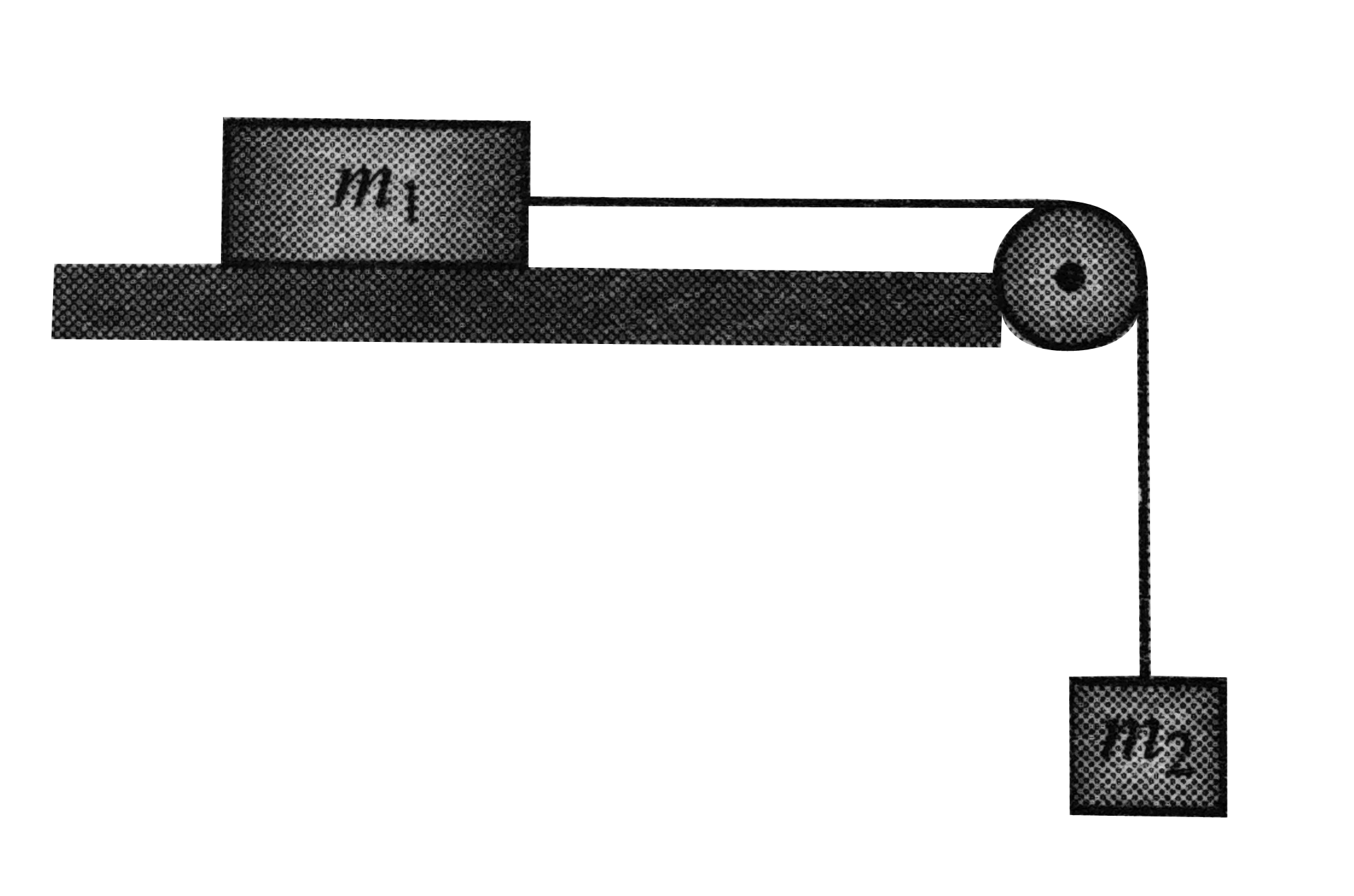
View SolutionTwo blocks are connected by a string, as shown in figure. They are released from rest. Show that after they have moved a distance L, their common speed is given by v=√2(m2−μm1)gL/(m1+m2), in which μ is the coefficient of kinetic friction between the upper block and the surface. Assume that the pulley is massless and frictionless.
View SolutionA block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?

View SolutionIn the system shown in figure, the block A is released from rest. Find
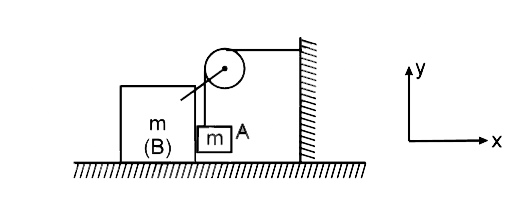
the acceleration of both blocks ‘A’ and ‘B’.
View Solution

