A block of mass m is suspened through a spring of spring constant k and is in equlibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium psitin, the block comes to an instantaneous rest?

l0: Natural length of spring when the block is in position (1),
The block is in equilibrium mg=kx0⇒x0=mgk
Now the block is given velocity v0 in upward direction.
Taking equilibrium position as the reference line between (1) and (2) mechanical energy conservation
12mv20+12kx20=12k(h−x0)2+mgh
=12kh2+12kx20−khx0+mgh
12mv20=12kh2−kh×mgk+mgh
=12kh2
h=v0√mk
(b) 
12mv20+12kx20=12k(h+x0)2−mgh
Solving as above
h=v0√mk
Topper's Solved these Questions
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
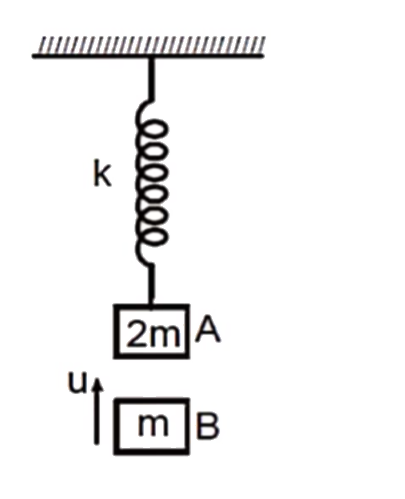
View Solution
Knowledge Check
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
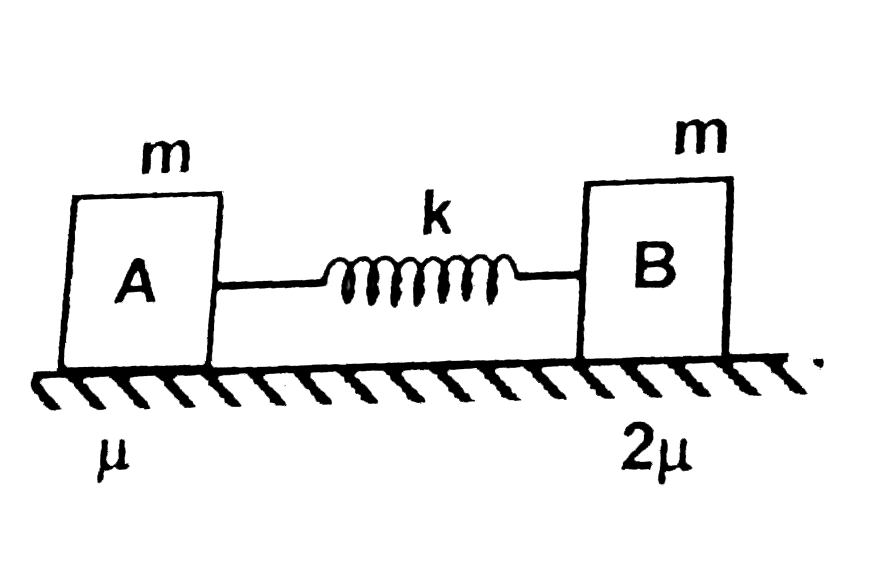 A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A2μg√2mkBμg√2mkCμg√mkD2μg√m2kA block of mass m=0.1kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
A0.6 JB0.8 JC1.5 JD0.3 J
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionConsider the spring blcok system shoen in the figure initially block m is in equlibrium. An impulse gives the block a velocity v upwards. Find the maximum speed of the block during the motion.
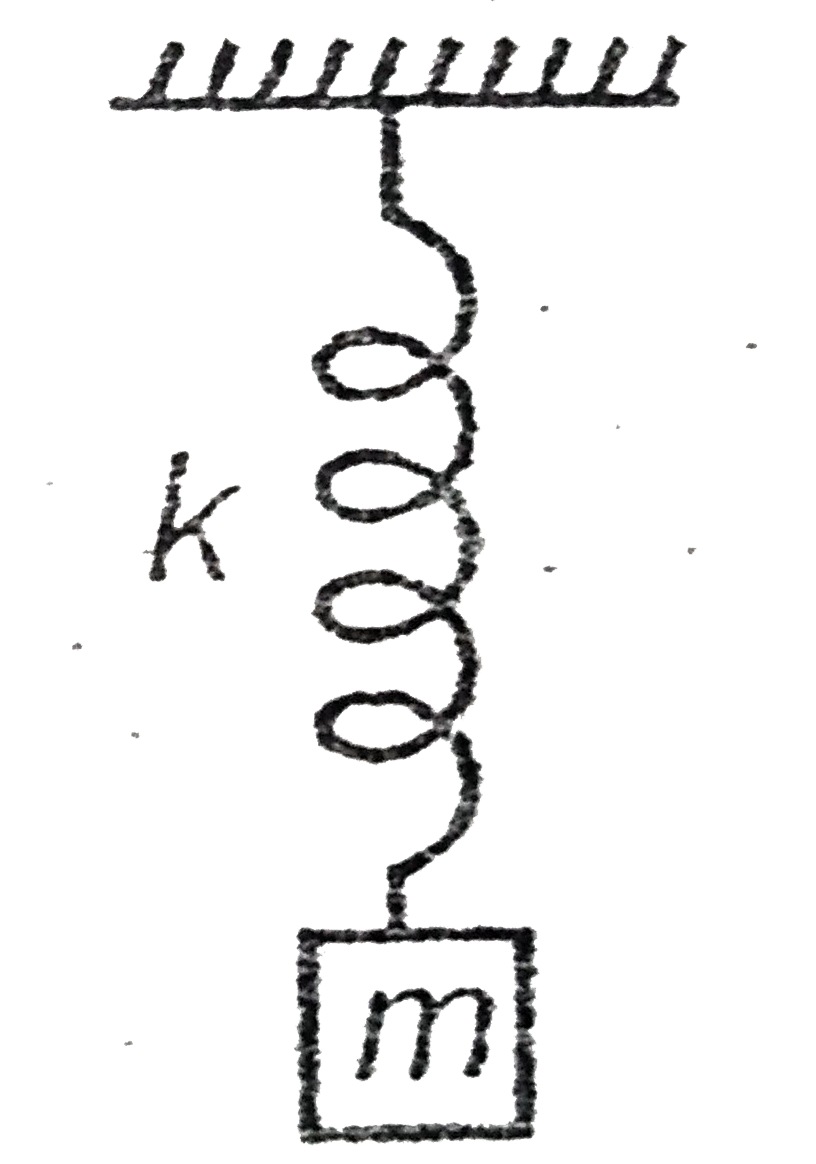
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution