A particle is thrown with speed $u$ at an angle $θ$ with horizontal.

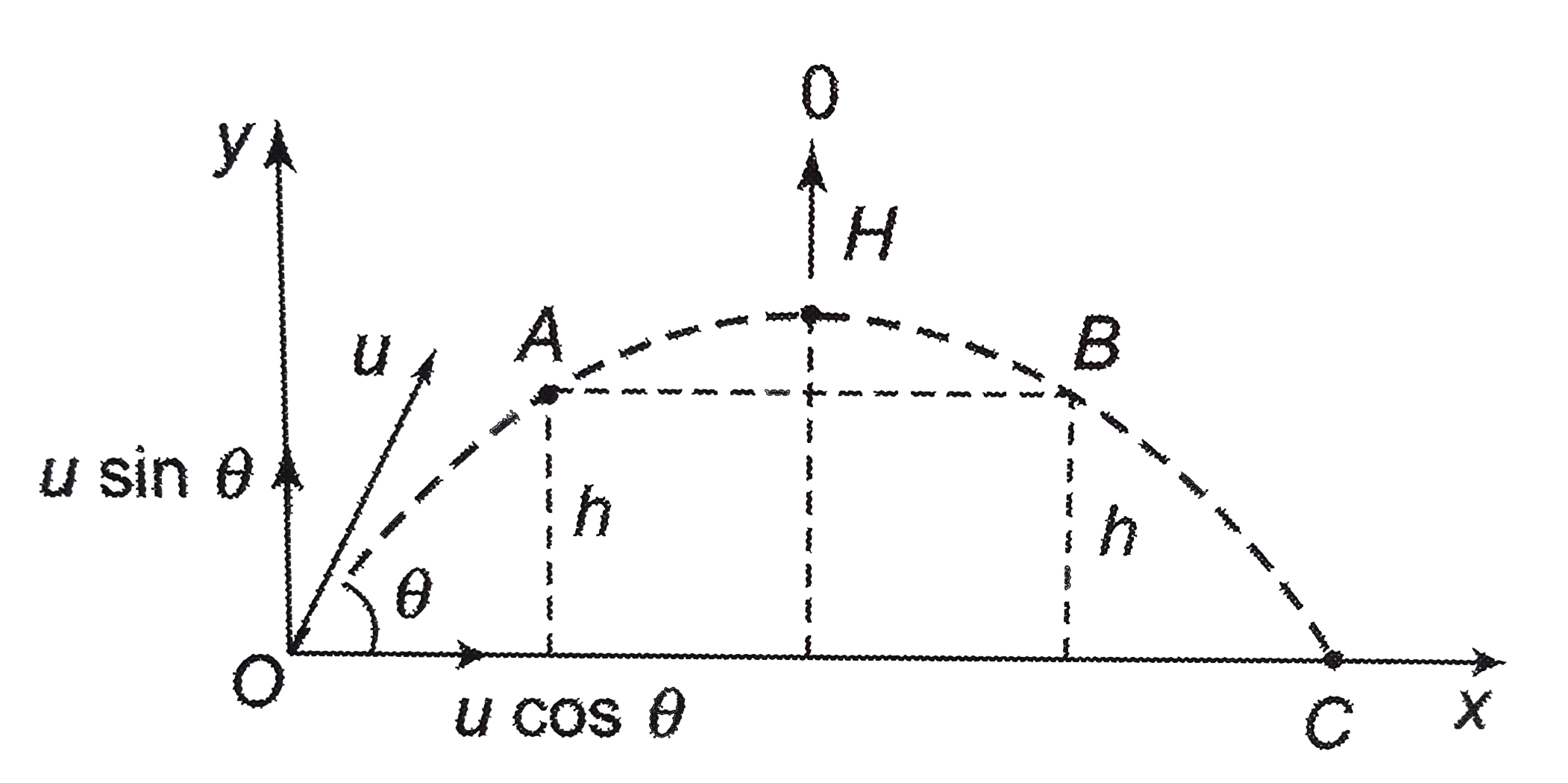
Find the average velocity of particle:
(a) $O$ to $C$ (b) $A$ to $B$ ( c) $O$ to $H$

Video Solution

Text Solution

Verified by Experts

(a) $O$ to $C$ : Displacement in vertical direction $= 0$ , hence ${¯ v}_{y} = 0$ .
In the horizontal direction, velocity is constant, hence
${¯ v}_{x} = u cos θ$
$¯ v = {¯ v}_{x} = u cos θ$
(b) $A$ to $B$ : Since the vertical distance between $A$ and $B = 0$ ltbgt ${¯ v}_{y} = 0, {¯ v}_{x} = u cos θ, ¯ v = u cos θ$
( c) $O$ to $H$ : ${¯ v}_{x} = u cos θ$
${¯ v}_{y} = \frac{H_{max}}{\frac{T}{2}} = \frac{u sin θ}{2}$
or ${¯ v}_{y} = \frac{u sin θ + 0}{2} = \frac{u sin θ}{2}$
$v = \sqrt{{¯ v}_{x}^{2} + {¯ v}_{y}^{2}} = \frac{u}{2} \sqrt{1 + 3 {cos}^{2} θ}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is thrown with speed $u$ at an angle of projection $θ$ with horizontal as shown.

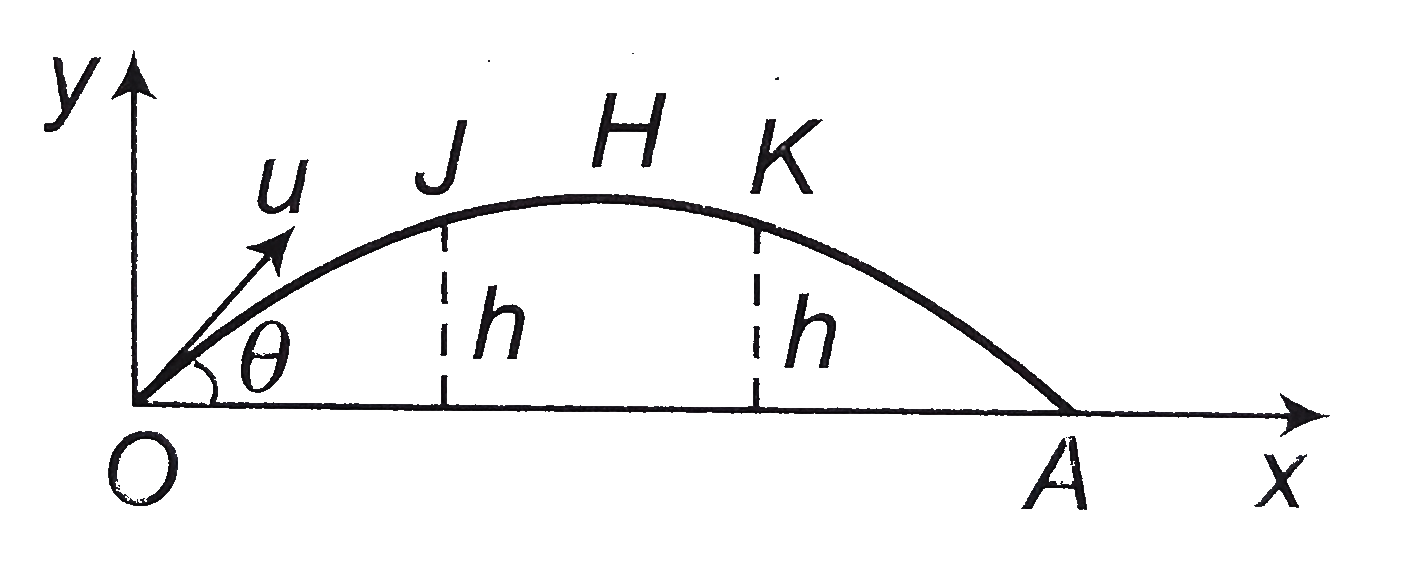
(i) The avergae velocity of particle from $O$ to $A$ is $u cos θ$
(ii) The average velocity of particle from $O$ to $H$ (highest point) is $\frac{u}{2} \sqrt{1 + 3 {cos}^{2} θ}$
(iii) The average velocity of particle from $J$ to $K$ is $u cos θ$
(iv) The angle between the velocity and the acceleration between $O$ and $H$ is greater than $90^{\circ}$ , between $H$ to $A$ is less than $90^{\circ}$ and at highest point is $90^{\circ}$
A(i), (ii)
B(i), (iii)
C(ii), (iv)
Dall option are correct
Question 2 - Select One
A particle is thrown with a speed $u$ at an angle $θ$ with horizontal. After how much time the velocity of particle will be perpendicular to the initial motion of direction
A $\frac{u}{g cos θ}$
B $\frac{u}{g sin θ}$
C $\frac{u sin θ}{g}$
D $\frac{u cos θ}{g}$
Question 3 - Select One
A particle is projected with speed $u$ at angle $θ$ to the horizontal. Find the radius of curvature at highest point of its trajectory
A $\frac{u^{2} {cos}^{2} θ}{2 g}$
B $\frac{\sqrt{3} u^{2} {cos}^{2} θ}{2 g}$
C $\frac{u^{2} {cos}^{2} θ}{g}$
D $\frac{\sqrt{3} u^{2} {cos}^{2} θ}{g}$

CP SINGH-MOTION IN A PLANE-Exercises

Home
Ask Doubt
Profile