If n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
ΔSsys=−2.303nRlog(P1p2)
ΔSsys=2.303Rnlog(P1p2)
ΔSsys=−2.303Rnlog(P1p2)
ΔSsys=2.303nRlog(P1p2)
The correct Answer is:D
Because the internal energy of an ideal gas is a function of temperature only,
ΔU=0
Therefore, according to the first law of thermodynamics we have
ΔU=0qrev+W
or qrev=−W=2.303nRTlog(V2V1)
According to Boyle's law,
p1v1=v2V2
or p1p2=V2V1
qrev=2.303nRTlog(p1p2)
ΔSsys=qsys, revT
=2.303nRlog(p1p2)
Topper's Solved these Questions
- THERMODYNAMICSBook:R SHARMAChapter:THERMODYNAMICSExercise:Follow - up Test 10
Explore 10 Videos
- THERMODYNAMICSBook:R SHARMAChapter:THERMODYNAMICSExercise:Ouestion Bank Level I
Explore 8 Videos
- THERMODYNAMICSBook:R SHARMAChapter:THERMODYNAMICSExercise:Follow - up Test 8
Explore 7 Videos
- THE S BLOCK ELEMENTSBook:R SHARMAChapter:THE S BLOCK ELEMENTSExercise:ARCHIVES
Explore 27 Videos
Similar Questions
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which relation is correct (γ=CPCV)?
View Solution
Knowledge Check
n moles of gas in a cylinder under a piston is transferred infinintley slowly from a state with a volume of V0 and a pressure 3P0 to a state with a volume of 3V0 and a pressure P0 as shown in Fig. The maximum temperature that gas will reach in this process is
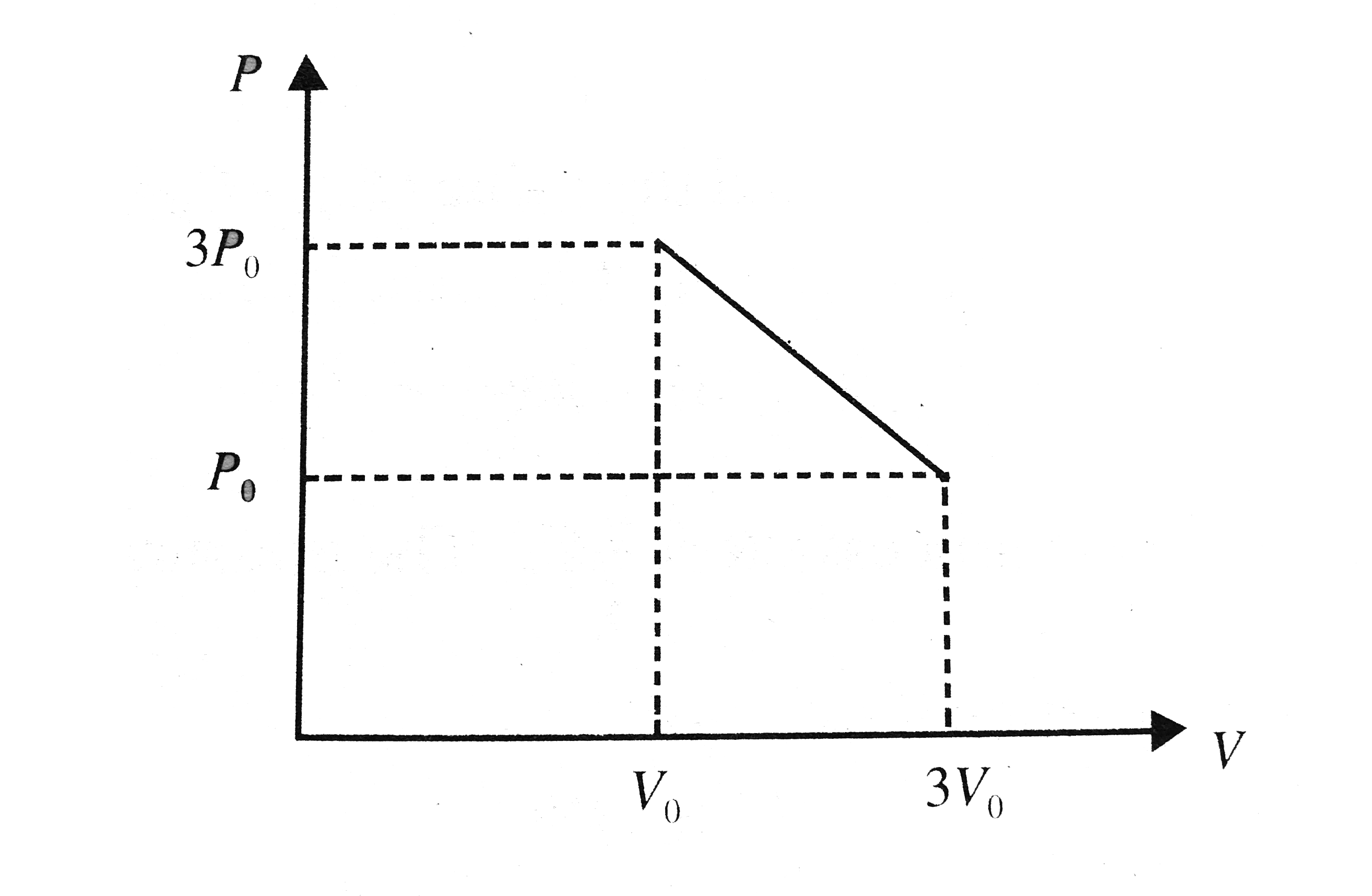 AP0V0nRB3P0V0nRC4P0V0nRD2P0V0nR
AP0V0nRB3P0V0nRC4P0V0nRD2P0V0nRA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) isAwadi=wisoBwadi<wisoCwadi=2wisoDwadi>wisoA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which of the following is correct?AP1V1=P2V2BP1/P2=V1/V2CP1/P2=P1/P3DP1=P2
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.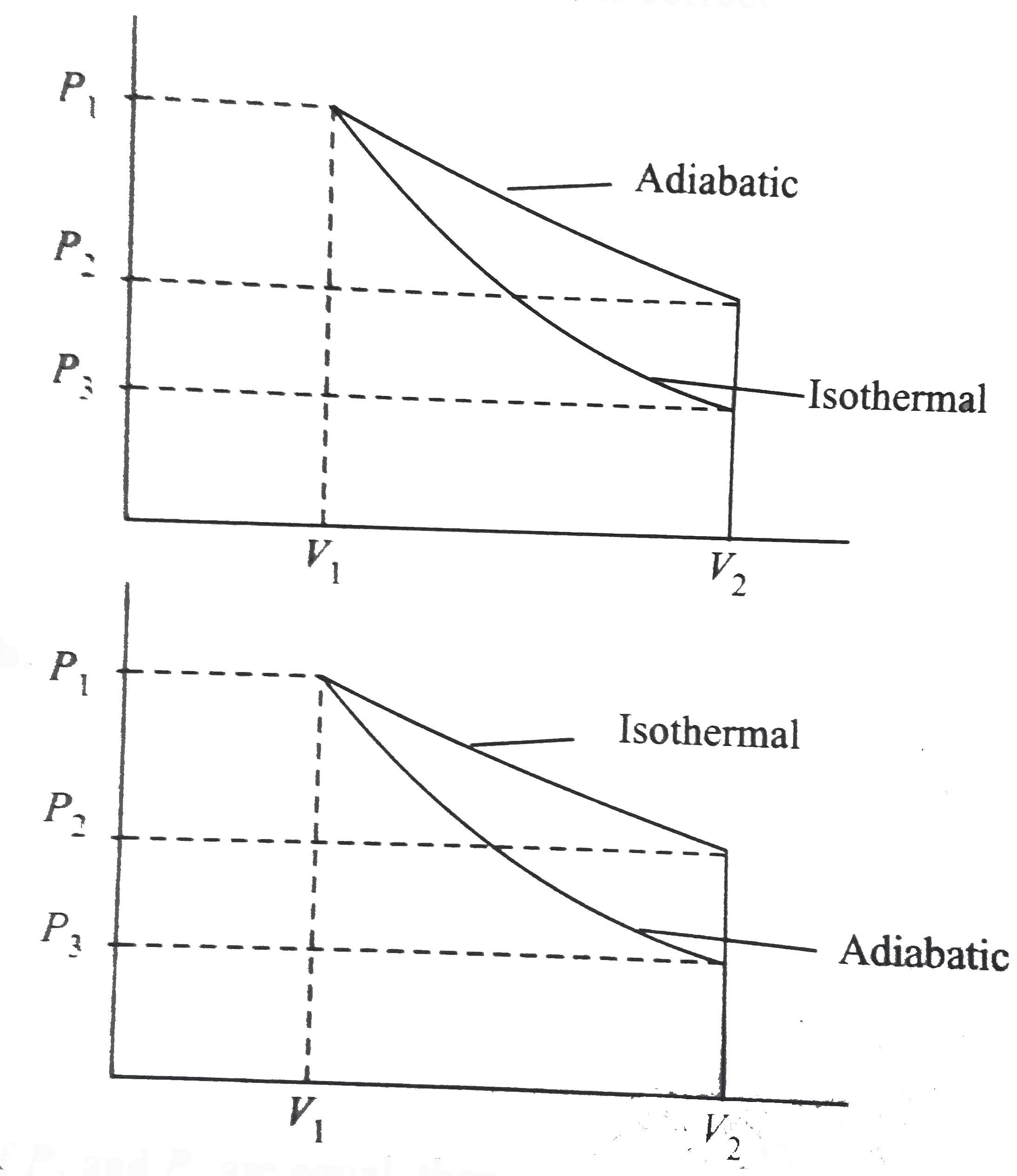
View SolutionThe initial volume of an ideal gas is V1 and the initial pressure is P1=6 atmosphere. It expands isothermally to a volume V2 and pressure P2=3atm, and then adiabatically to a volume V3 and pressure P3=2atm. Draw a rough sketch of these changes. Calculate the value of V2/V1andV3/V2.
Take γ=1.4.
View SolutionA certain mass of an ideal gas at pressure P1 is adiabatically expanded from an initial volume V1 to a final volume V2. The resulting pressure P2 of the gas is given by:
View SolutionThe change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2<T) is equal to
View SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
View Solution

