If L is the inductance, 'I' is current in the circuit, 12Li2 has the dimesions of
Work
Power
Pressure
Force
The correct Answer is:A
To find the dimensions of the expression 12LI2, where L is inductance and I is current, we can follow these steps:
Step 1: Identify the dimensions of inductance L
The dimension formula for inductance L is given by:
(L)=ML2T−2I−2
where M is mass, L is length, T is time, and I is electric current (in amperes).
Step 2: Identify the dimensions of current I
The dimension of current I is:
(I)=I
Step 3: Calculate the dimensions of I2
Since we need I2, we square the dimension of current:
(I2)=I2
Step 4: Combine the dimensions of L and I2
Now, we can combine the dimensions of L and I2:
Dimensions of 12LI2=(L)⋅(I2)=(ML2T−2I−2)⋅(I2)
Step 5: Simplify the expression
When we multiply the dimensions, we get:
ML2T−2I−2⋅I2=ML2T−2
Step 6: Final result
Thus, the dimensions of 12LI2 are:
ML2T−2
This is the dimension of work or energy.
The dimension formula for inductance L is given by:
(L)=ML2T−2I−2
where M is mass, L is length, T is time, and I is electric current (in amperes).
The dimension of current I is:
(I)=I
Since we need I2, we square the dimension of current:
(I2)=I2
Now, we can combine the dimensions of L and I2:
Dimensions of 12LI2=(L)⋅(I2)=(ML2T−2I−2)⋅(I2)
When we multiply the dimensions, we get:
ML2T−2I−2⋅I2=ML2T−2
Thus, the dimensions of 12LI2 are:
ML2T−2
This is the dimension of work or energy.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-I (C.W)
Explore 42 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-II (C.W)
Explore 28 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- VECTORSBook:NARAYNAChapter:VECTORSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
If L denotes the inductance of an inductor through which a current i is flowing, the dimensions of Li2 are
AML2T−2BNot expressible in MLTCMLT−2DM2L2T−2If C,R,L and I denot capacity resitance, inductance and electric current respecitively, the quantities having the same dimensions of time are
(a) CR, (b) L/R, (c) √L/C, (d) LI2Aa and b onlyBa and c onlyCa and b onyDa,b and c onlyIn the given circuit the current l is
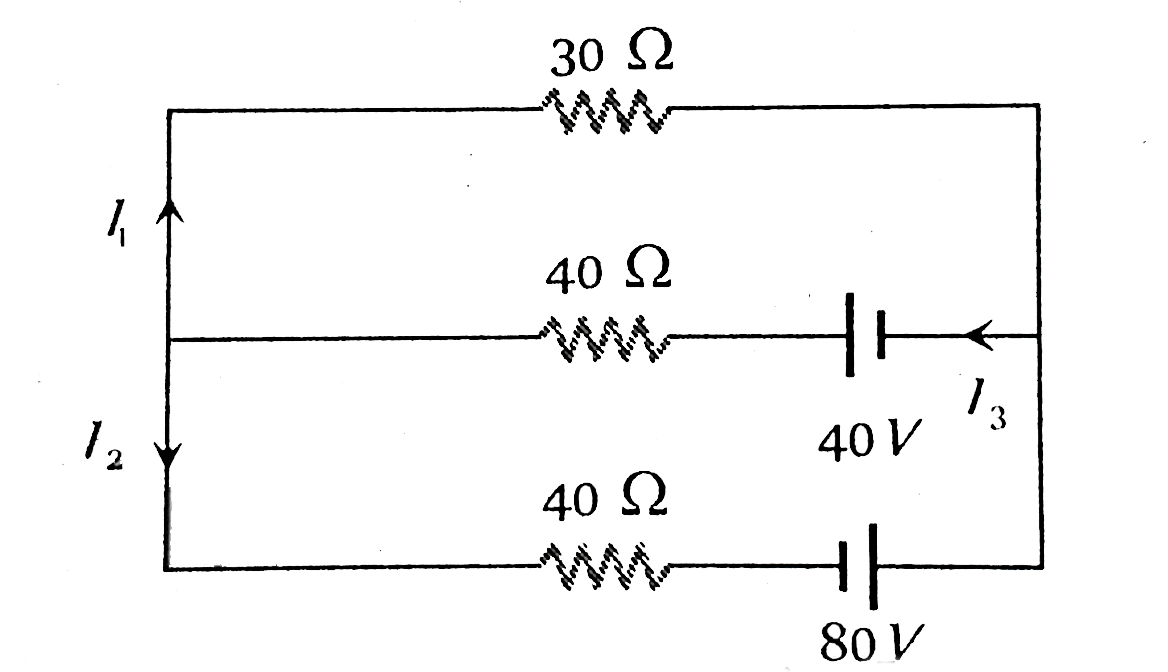 A0.4AB−0.4AC0.8AD−0.8A
A0.4AB−0.4AC0.8AD−0.8A
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionWhen current i passes through an inductor of self inductance L, energy stored in it is 1/2.Li2. This is stored in the
View SolutionIn a purely inductive circuit, the current is
View SolutionIn the circuit given, find the currents I, I1 and I2 in the circuit.
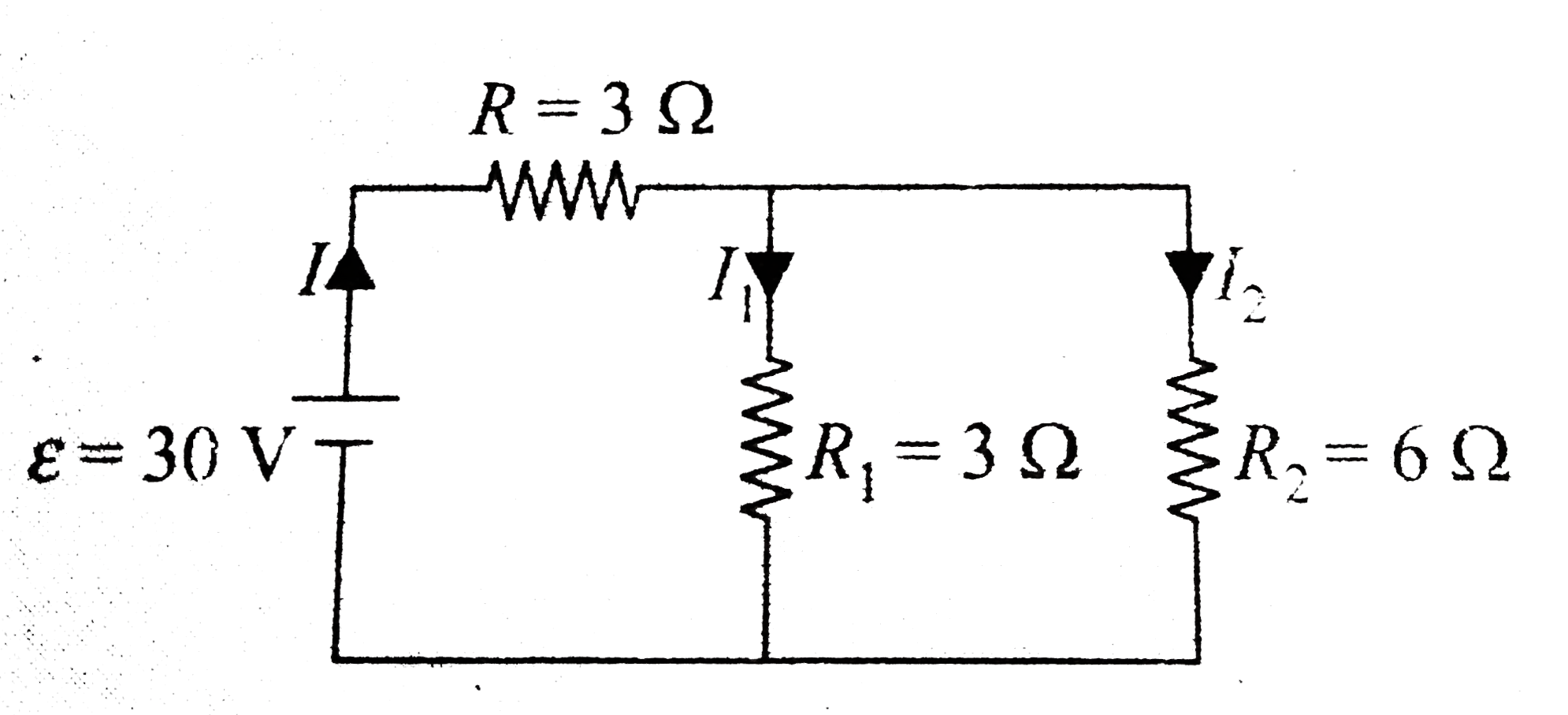
View SolutionAssertion (A) : The inductive reactance limits the currents in a purely inductive circuit in the same way as the resistancefsd circuit.
Reason (R ) : The inductive reactance is directly propontional to the inductance and to the frequency of tha varying current.
View Solution

