Calculate the gravitational potential at the centre of base of a solid hemisphere of mass M, radius R.
Consider a hemispherical shell of radius r and thickness dr. Its mass is given by
dmM23πR3(2πr2dr)=3Mr2drR3
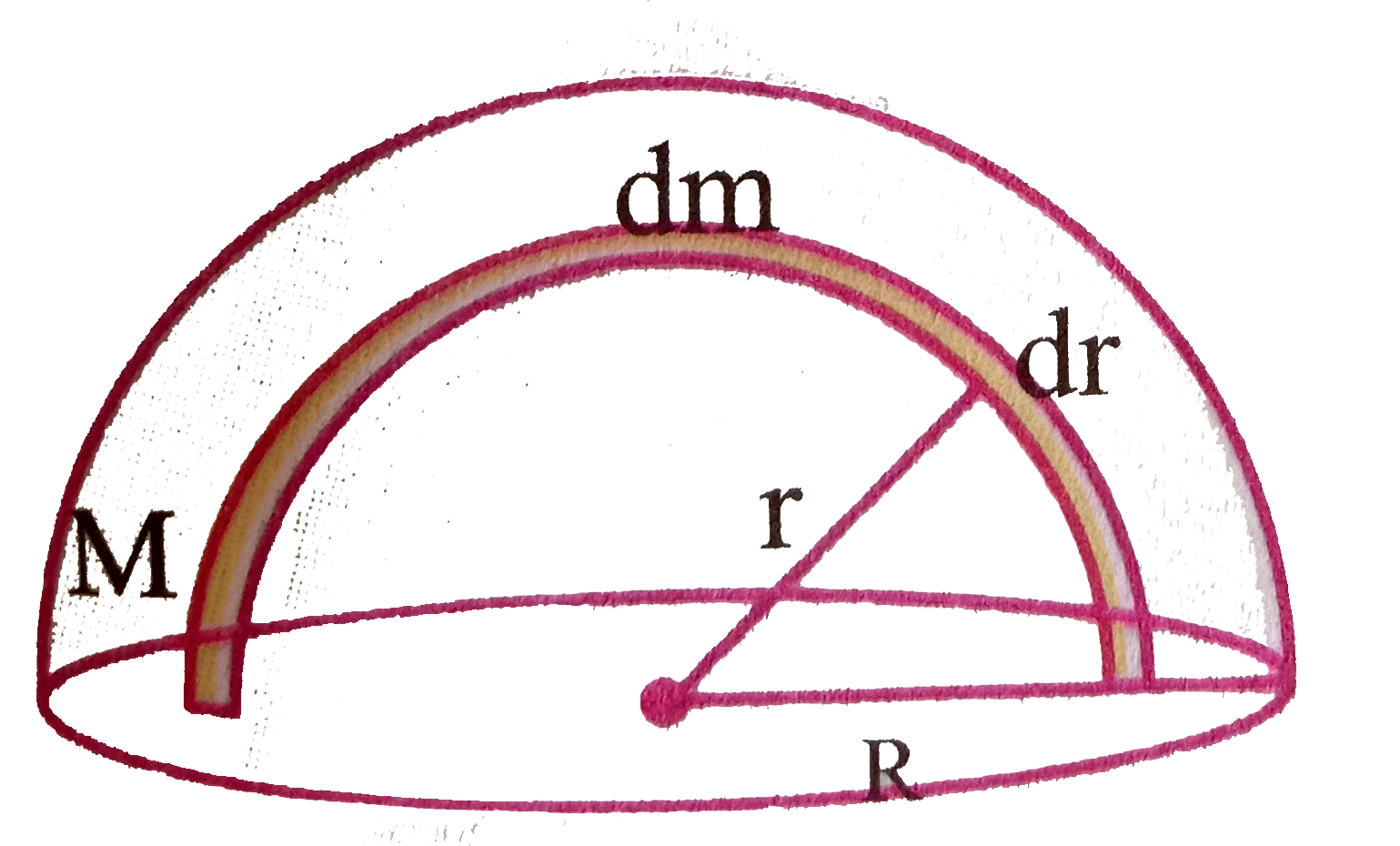
Since all points of this hemispherical shell are at the same distance r from centre O, potential at O due to it is
dV=−Gdmr=−3GMrdrR3
∴V=∫R0dV=−3GM2R
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:C.U.Q
Explore 220 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL I(C.W.)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Calculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View Solution
Knowledge Check
The total surface area of a solid hemisphere of radius r is
Aπr2B2πr2C3πr2D4πr2Find distance of centre of mass of solid hemisphere of radius 8cm from centre
A3 cmB3/8 cmC4 cmD2 cm
The centre of gravity of a solid hemisphere of radius a is
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionThe centre of gravity of a solid hemisphere of radius a is : (A)
View SolutionDetermine the position of the centre of mass of a hemisphere of radius R.
View SolutionCalculate the self-gravitational potential energy of matter forming a. a thin uniform shell of mass M and radius R, b. a uniform sphere of mass m and radius R.
View SolutionA particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity.
What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
View Solution

