A particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them

consider an elementof mass 'dm' and length 'dx' at a distance 'x' from the point mass. Mass of the element dm=MLdx.
Gravitational force on 'm' due to this elements is dF=Gm(MLdx)x2,F=∫(d+L)dGm(ML)dxx2
⇒F=GmML∫(d+L)dx−2dx=GmML[x−1−1](d+L)d
⇒F=GmML[−1x](d+L)d=GmML[1d−1(d+L)]
F=GmML[d+L−d(d+L)d]=GmMa(a+L)
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:C.U.Q
Explore 220 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL I(C.W.)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
A mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution
Knowledge Check
A point mass is placed at a distance a from one end of a rod of mass M and length l on the line which passes through the central axis of the rod. The potential energy of the system.
AU=−GMmaloge(a+1a)BU=−GMm(1a−1a+1)CU=−GMm1loge(a+1a)DU=−GMmaTwo particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
AzeroB7Gm4r2C9Gm4r2D3Gm2r2A point mass M is at a distance S from an infinitely long and thin rod of linear density D. If G is the gravitational constant then gravitational force between the point mass and the rod is
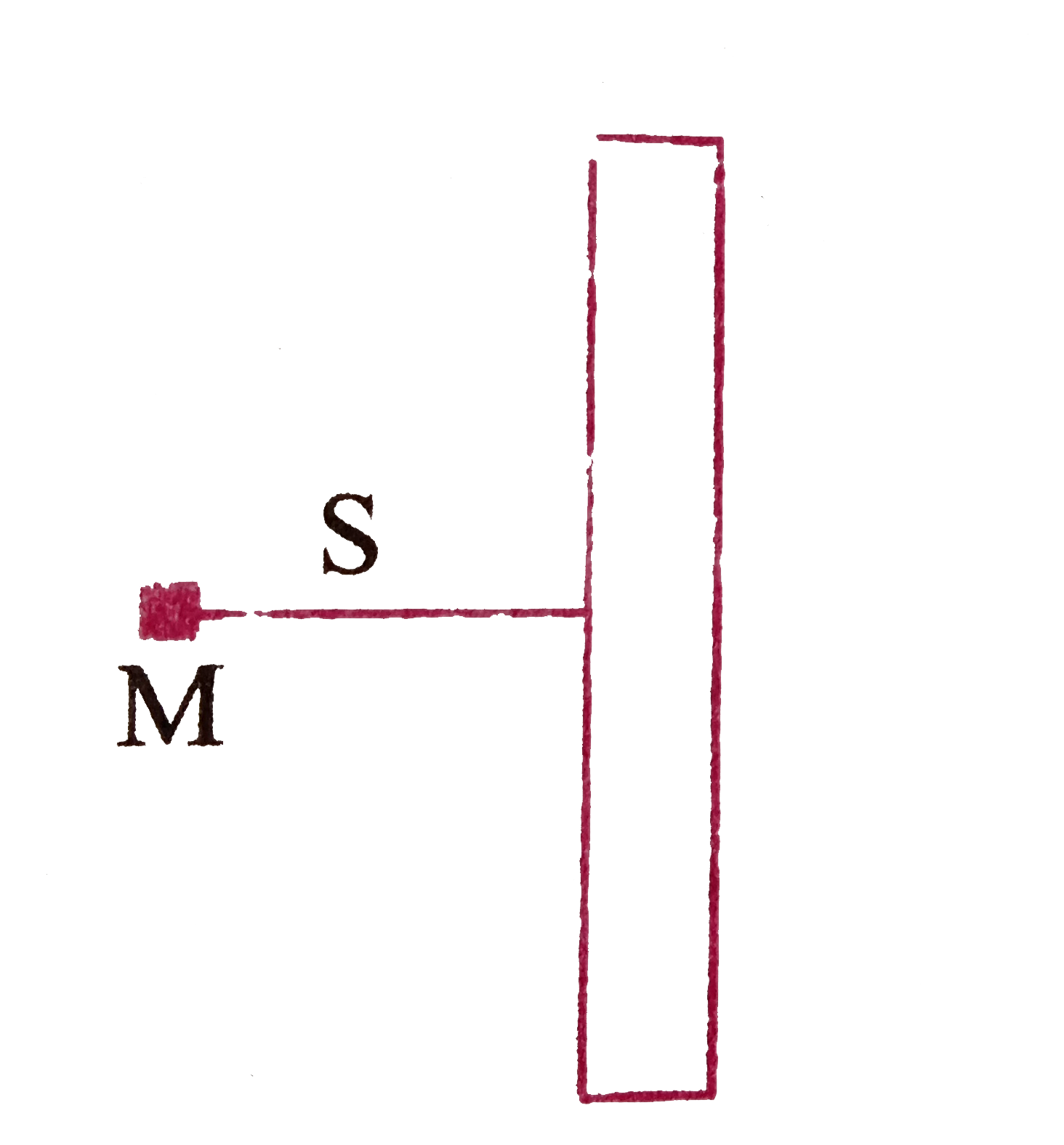 A2GMDSBMGDSCMGD2SD23MGDS
A2GMDSBMGDSCMGD2SD23MGDS
A particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionConsider the situation as shown in the following diagrams. Find net gravitational force on the particle of mass m.

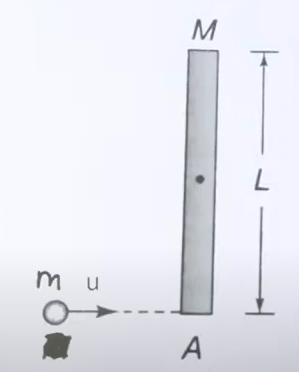
View SolutionA particle of mass m and speed u collides elastically with the end of a uniform rod of mass M and length L as shown. If the particle comes to rest after collision, find mM
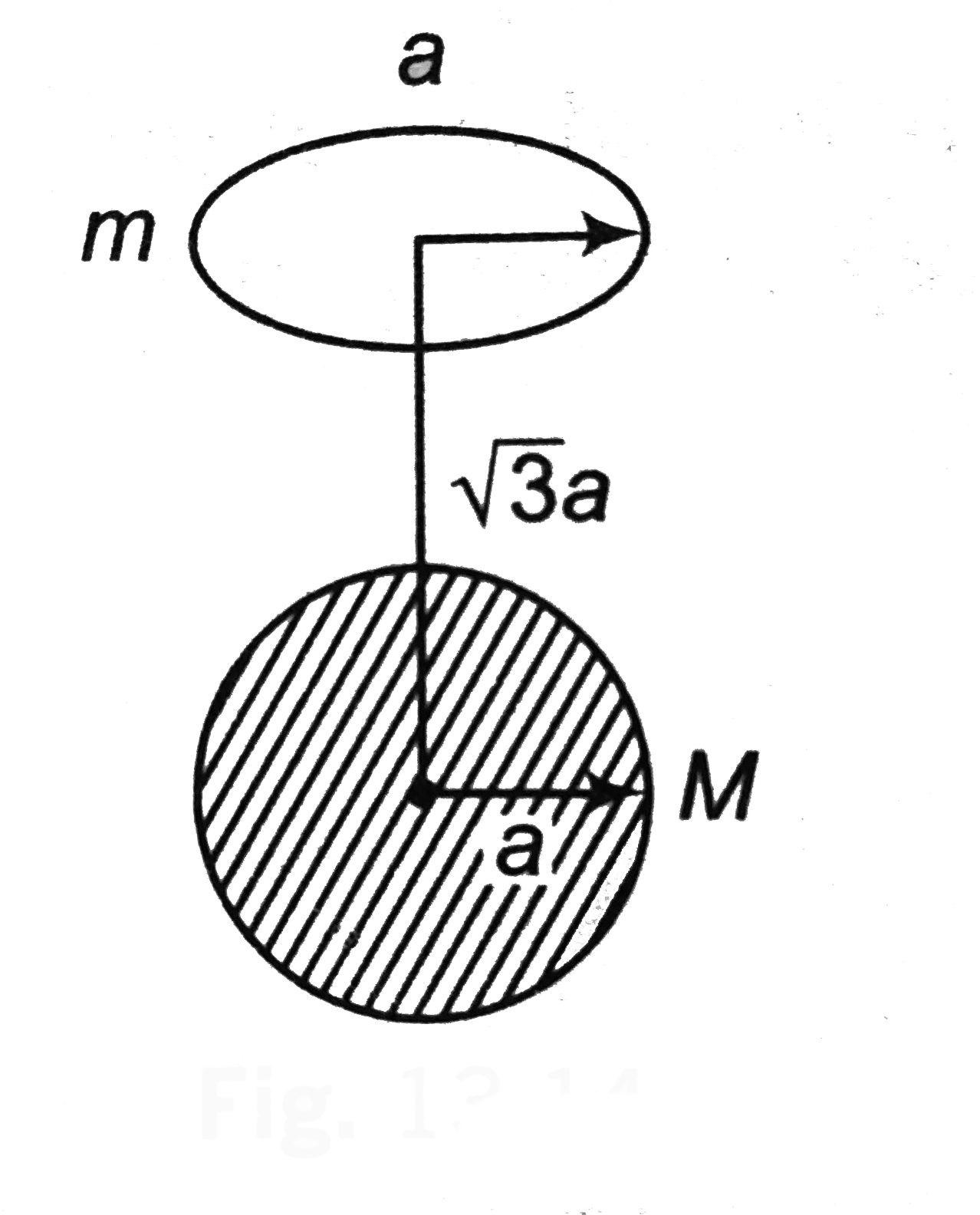
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View Solution

