Assertion : An emf →E is induced in a closed loop where magnetic flux is varied. The induced →E is not a conservative field.
Reason : The line intergral →E.→dl around the closed loop is non-zero.
If both assertion and reason are true and the reason is the correct explanation of the assertion.
If both assertion and reason are true but reason is not the correct explanation of the assertion.
If asserction is true but reason is false.
If asserction is false but reason is true.
The correct Answer is:A
Step by step video, text & image solution for Assertion : An emf vec(E) is induced in a closed loop where magnetic flux is varied. The induced vec(E) is not a conservative field. Reason : The line intergral vec(E).vec(dl) around the closed loop is non-zero. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:TARGET PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EVALUATION TEST
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:TARGET PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CRITICAL THINKING
Explore 84 Videos
- ELASTICITYBook:TARGET PUBLICATIONChapter:ELASTICITYExercise:Evaluation test
Explore 14 Videos
- ELECTROSTATICSBook:TARGET PUBLICATIONChapter:ELECTROSTATICSExercise:EVALUATION TEST
Explore 14 Videos
Similar Questions
Assertion : An electrostatic field line never form closed loop.
Reason : Electrostatic field is a conservative field.
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
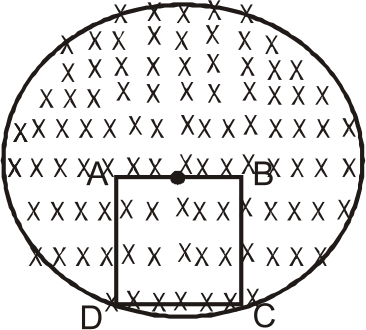
View Solution
Knowledge Check
To induce an e.m.f. in a coil, the linking magnetic flux
AMust decreaseBCan either increase or decreaseCMust remain constantDMust increaseThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
AIf ϕ=0,e must be 0BIf ϕ≠0,e cannot be 0CIf e is not 0,ϕ may or may not be 0DNone of the above is correctFigure. shows three rigions of magnetic field each of area A, and in each rigion, magnitude of mqagnetic field decreases rate α. If →E is the induced electric field, then the vlue of the line ∮→E.d→r along the given loop is equal to
 A(a) αAB(b) −αAC( c) 3αAD(d) −3αA
A(a) αAB(b) −αAC( c) 3αAD(d) −3αA
Asseration: The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason: The emf is induced due to change in magnetic flux.
View SolutionAsseraton: The work done by a charge in a closed (induced) current carrying loop is non-zero.
Reason: Induced electric field is non-conservative in nature.
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

The magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate α tesla/sec The graph showing the variation.of induced electric field with distance r from the axis of cylinder is :
View SolutionA: The electric field induced due to changing magnetic field is non-conservative,
R: The line integral of the electric field induced due to changing magnetic field along a closed loop is always zero.
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

Refer to above questions, Find the magnitude of line integral of induced electric field along path CD.
View Solution

