A body of mass 6.28 kg is suspended from one end of a wire of length 10 m. The radius of the wire is changing uniformly from 19.6×10−4m at one end to 10×10−4m at the order end. Find the change in the length of the wire.
[Y=2×1011N/m2]
0.1 mm
0.3 mm
0.5 mm
0.7 mm
The correct Answer is:C
To solve the problem of finding the change in length of a wire with a varying radius under a load, we can follow these steps:
Step 1: Understand the Problem
We have a wire of length L=10m and a mass m=6.28kg suspended from one end. The radius of the wire varies linearly from r1=19.6×10−4m at one end to r2=10×10−4m at the other end.
Step 2: Calculate the Force
The force F acting on the wire due to the suspended mass is given by:
F=m⋅g
where g≈9.8m/s2. Thus,
F=6.28kg×9.8m/s2=61.544N≈62.8N
Step 3: Define the Radius as a Function of Position
Since the radius varies linearly, we can express the radius r(x) at a distance x from the top as:
r(x)=r1−(r1−r2L)x
Substituting r1 and r2:
r(x)=19.6×10−4−(19.6×10−4−10×10−410)x
r(x)=19.6×10−4−0.96×10−4x
Step 4: Calculate the Cross-Sectional Area
The cross-sectional area A of the wire at position x is:
A(x)=π(r(x))2=π(19.6×10−4−0.96×10−4x)2
Step 5: Use Young's Modulus
The elongation ΔL of the wire can be calculated using the formula:
ΔL=∫L0FA(x)Ydx
where Y=2×1011N/m2 is the Young's modulus.
Step 6: Substitute and Integrate
Substituting the values:
ΔL=∫10062.8π(19.6×10−4−0.96×10−4x)2(2×1011)dx
Step 7: Solve the Integral
This integral can be solved using standard calculus techniques. The result will yield the total elongation of the wire.
Step 8: Calculate the Final Result
After performing the integration, we find:
ΔL≈0.5099mm
Final Answer
The change in the length of the wire is approximately 0.5099mm.
---
We have a wire of length L=10m and a mass m=6.28kg suspended from one end. The radius of the wire varies linearly from r1=19.6×10−4m at one end to r2=10×10−4m at the other end.
The force F acting on the wire due to the suspended mass is given by:
F=m⋅g
where g≈9.8m/s2. Thus,
F=6.28kg×9.8m/s2=61.544N≈62.8N
Since the radius varies linearly, we can express the radius r(x) at a distance x from the top as:
r(x)=r1−(r1−r2L)x
Substituting r1 and r2:
r(x)=19.6×10−4−(19.6×10−4−10×10−410)x
r(x)=19.6×10−4−0.96×10−4x
The cross-sectional area A of the wire at position x is:
A(x)=π(r(x))2=π(19.6×10−4−0.96×10−4x)2
The elongation ΔL of the wire can be calculated using the formula:
ΔL=∫L0FA(x)Ydx
where Y=2×1011N/m2 is the Young's modulus.
Substituting the values:
ΔL=∫10062.8π(19.6×10−4−0.96×10−4x)2(2×1011)dx
This integral can be solved using standard calculus techniques. The result will yield the total elongation of the wire.
After performing the integration, we find:
ΔL≈0.5099mm
The change in the length of the wire is approximately 0.5099mm.
Topper's Solved these Questions
- ELASTICITYBook:TARGET PUBLICATIONChapter:ELASTICITYExercise:Competitive Thinking
Explore 69 Videos
- CURRENT ELECTRICITY Book:TARGET PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:Evaluation Test
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:TARGET PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EVALUATION TEST
Explore 8 Videos
Similar Questions
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
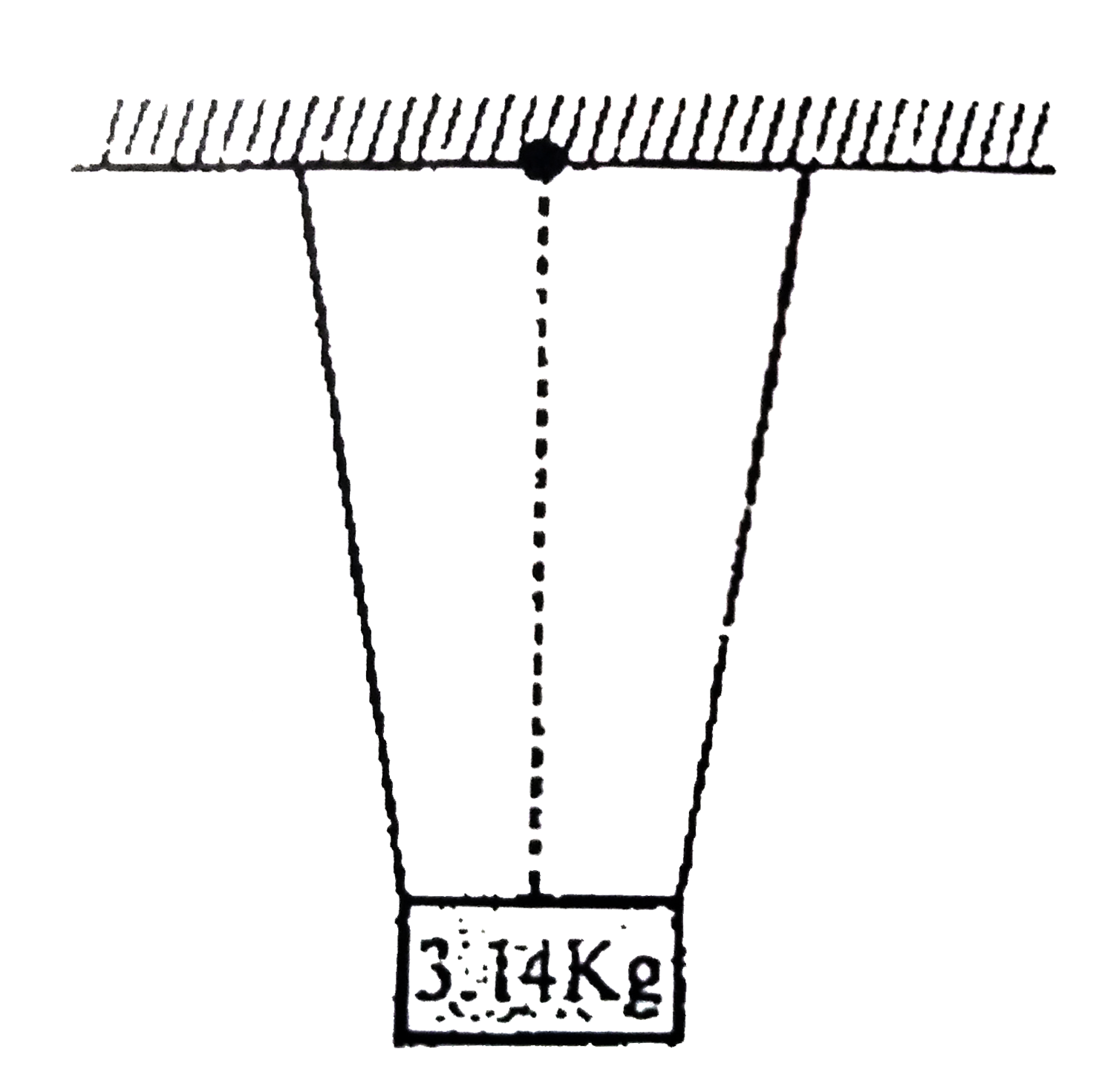
View SolutionA wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View Solution
Knowledge Check
A body of mass 3.14kg is suspended from one end of a wire of length 10m. The radius of cross-section of the wire is changing uniformly from 5×10−4m at the top (i.e. point of suspension) to 9.8×10−4m at the bottom . Young's modulus of elasticity is 2×1011N/m2. The change in length of the wire is
A4×10−3mB3×10−3mC10−3mD2×10−3mA body of mass 1 kg is fastened to one end of a steel wire of cross- section area 3×10−6m2 and is rotated in horizantal circle of radius 20 cm with a constant speed 2m/s. Find the elongation of the wire (Y=2×1011N/m2)
A0.33×10−5mB0.67×10−5mC2×10−5mD4×10−5One end of a wire 2 m long and dameter 2 mm is fixed in a celling . A naughty boy of mass 10 kg jumps to catch the free end and stays, there. The chamge is length of wire is (Taker=10m/s2,Y=2×1011N/m2)
A3.185×10−5B2 mmC3 mmD4mm
One end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceilign and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionAn iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
View SolutionA body of mass 1 kg is attached to one end of a wire and rotated in a horizontal circle of diameter 40 cm with a constant speed of 2m/s. What is the area of cross-section of the wire if the stress developed in the wire is 5×106N/m2 ?
View SolutionA body of mass 500 g is fastened to one end of a steel wire of length 2m and area of cross-section 2mm2. If the breaking stress of the wire is 1.25×107N/m2, then the maximum angular velocity with which the body can be rotated in a horizontal circle is
View SolutionA uniform nickel wire of length 3.14 m and radius 10−3 hangs vertically. If a mass of 20 kg is attached to its free end. The extension in the wire is,
(Young's modulus of nickel =20×1010N/m2)
View Solution

