A body of mass 1 kg is attached to one end of a wire and rotated in a horizontal circle of diameter 40 cm with a constant speed of 2m/s. What is the area of cross-section of the wire if the stress developed in the wire is 5×106N/m2 ?
2mm2
3mm2
4mm2
5mm2
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Given Data:
- Mass of the body, m=1kg
- Diameter of the circle, d=40cm=0.40m
- Radius of the circle, r=d2=0.402=0.20m
- Speed of rotation, v=2m/s
- Stress developed in the wire, σ=5×106N/m2
Step 1: Calculate the Centripetal Force
The centripetal force F required to keep the mass moving in a circle is given by the formula:
F=mv2r
Substituting the known values:
F=1×(2)20.20=1×40.20=40.20=20N
Step 2: Relate Stress to Force and Area
Stress σ is defined as the force F per unit area A:
σ=FA
Rearranging this equation to solve for the area A:
A=Fσ
Step 3: Calculate the Area of Cross-section
Now substituting the values of force F and stress σ:
A=20N5×106N/m2=205×106=205×10−6=4×10−6m2
Step 4: Convert Area to mm²
To convert the area from m² to mm²:
A=4×10−6m2=4×10−6×(1000mm)2=4×10−6×106mm2=4mm2
Final Answer:
The area of cross-section of the wire is 4mm2.
---
- Mass of the body, m=1kg
- Diameter of the circle, d=40cm=0.40m
- Radius of the circle, r=d2=0.402=0.20m
- Speed of rotation, v=2m/s
- Stress developed in the wire, σ=5×106N/m2
The centripetal force F required to keep the mass moving in a circle is given by the formula:
F=mv2r
Substituting the known values:
F=1×(2)20.20=1×40.20=40.20=20N
Stress σ is defined as the force F per unit area A:
σ=FA
Rearranging this equation to solve for the area A:
A=Fσ
Now substituting the values of force F and stress σ:
A=20N5×106N/m2=205×106=205×10−6=4×10−6m2
To convert the area from m² to mm²:
A=4×10−6m2=4×10−6×(1000mm)2=4×10−6×106mm2=4mm2
The area of cross-section of the wire is 4mm2.
Topper's Solved these Questions
- ELASTICITYBook:MARVEL PUBLICATIONChapter:ELASTICITYExercise:Test Your Grasp - 5
Explore 15 Videos
- CURRENT ELECTRICITYBook:MARVEL PUBLICATIONChapter:CURRENT ELECTRICITYExercise:MCQ
Explore 151 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Book:MARVEL PUBLICATIONChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Exercise:TEST YOUR GRASP - 16
Explore 30 Videos
Similar Questions
A copper wire of negligible mass, 1m length and cross-sectional area 106m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).
View SolutionA 5 kg mass is attached to one end of a copper wire 2m long and 2mm in diameter. Calculate the leteral compression produced in it. Posisson's ration is 0.3 and Young's modulus of the meterial of the wire is 12.5×1010Nm−2
View Solution
Knowledge Check
A body of mass 1 kg is fastened to one end of a steel wire of cross- section area 3×10−6m2 and is rotated in horizantal circle of radius 20 cm with a constant speed 2m/s. Find the elongation of the wire (Y=2×1011N/m2)
A0.33×10−5mB0.67×10−5mC2×10−5mD4×10−5A metal wire of negligible mass, length 1 m and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed on the table. A ball of mass 2kg is attached to the other end of the wire. When the wire and the ball are rotated with angular velocity of 20 rad/s, it is found that the wire is elongated by 10−3m. If the Young's modulus of the metal is n×1011N/m2, then the value of n is
A6B8C9D10One end of a uniform wire of length 'L' and mass 'M' is attached rigidly to a point in the roof and a load of a mass 'm' is suspended from its lower end. If A is the area of cross-section of the wire then the stress in the wire at height 'x' from its lower end (x<L) is
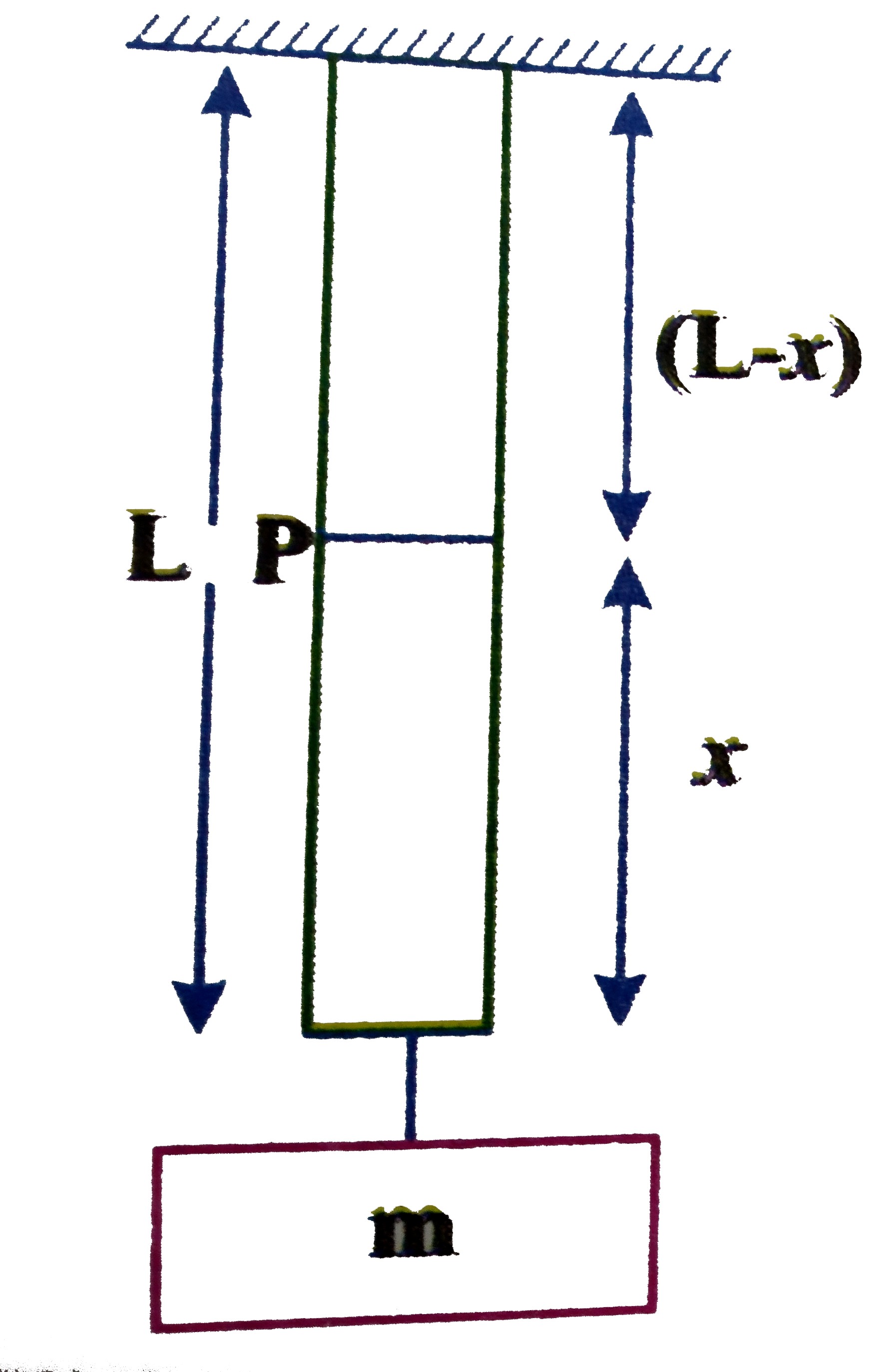 AMgA+mxgALBmgA−MxgALCmgA+MxgALDmgAL+MxgA
AMgA+mxgALBmgA−MxgALCmgA+MxgALDmgAL+MxgA
A stone of mass m is attached to one end of a wire of cross-sectional area A and Young's modulus Y. The stone is revolved in a horizontal circle at a speed such that the wire makes an angle θ with the vertical. The strain produced in the wire will be
View SolutionConsider a 1m long steel wire with the cross section of 0.05cm2 and Ysteel=2×1011Nm−2.Now a 15 kg mass is attached to the end of the wire and it is whirled in a vertical circle with an angular frequency of 2 rev/s at the bottom of the circle. When the mass is at the lowest point of its path, find the elongation of the wire in mm:
(Take g=10ms−2 & π2=10)
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight N is suspended from its lower end if s is the area of cross-section of the wire the stress in the wire at a height L4 from its lower end is
View SolutionA body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire =4.8×107Nm−2 and area of cross-section of a wire =10−2m2)
View Solution
