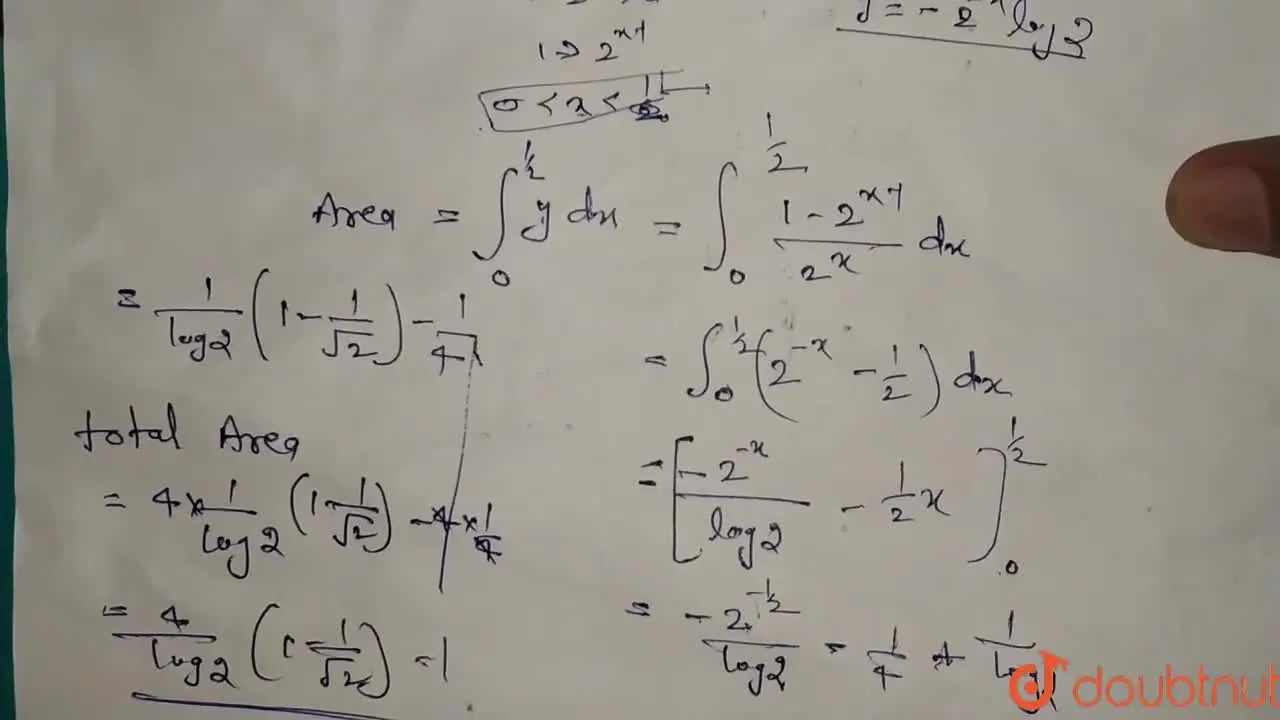Find the area of the region bounded by the curve 2|x||y|+2|x|−1≤1, with in the square formed by the lines |x|≤1/2,|y|≤1/2.
The correct Answer is:[4log2(1−2−1/2−1] sq units
Step by step video, text & image solution for Find the area of the region bounded by the curve 2^(|x|)|y|+2^(|x|-1)le1, with in the square formed by the lines |x|le1//2,|y|le1//2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Single Integer Answer Type Questions)8videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
BIONOMIAL THEOREM
Similar Questions
Find the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
View SolutionFind the area bounded by the curve |y|+12≤e−|x|.
View SolutionThe area of the region on place bounded by max (|x|,|y|)≤12 is
View SolutionFind the area bounded by the curves x2≤y≤x+2:
View SolutionFind the area of the region {(x,y):x2≤y≤x}
View SolutionFind the area of the region [ (x,y):x2≤y≤x)
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View SolutionThe area of the region bounded by the curves y2=4a2(x−1) and the lines x = 1 and y = 4a, is
View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
View SolutionThe aera of the region defined by ||x|−|y∣∣≤1andx2+y2≤1 in the xy plane is
View Solution