In a triangle If are points of trisection of prove that
The correct Answer is:D
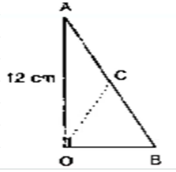
Step by step video, text & image solution for In a triangle O A B ,\ /_A O B=90^0dot If P\ a n d\ Q are points of trisection of A B prove that O P^2+O Q^2=5/9A B^2dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
In a triangle OAB, ∠AOB=900. If P and Q are points of trisection of AB prove that OP2+OQ2=59AB2.
View SolutionIn a triangle OAB,∠AOB=900. If P and Q are points of trisection of AB, prove that OP2+OQ2=59AB2
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionA line x+3y=12 cuts the xandy axis in AandB respectively. If PandQ being the points of trisection of AB(P being closer to A) and m1,m2 are the slope of the lines OP and OQ respectively ('O' is the origin), then m2=2m1 (b) m2=3m1 m2=4m1 (d) m2=5m1
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
 View Solution
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn Figure, BE⊥AC, AD is any line from A → BC intersecting BE in H.P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIf AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View Solution
