O is fixed point on the straight line traced out by a moving particle. If the distance of the particle from O at time t be (acosnt+bsinnt) [ a,b and n are constants]., show that the acceleration of the particle varies as its distance from O.Solution in Bengali
Step by step video & image solution for O is fixed point on the straight line traced out by a moving particle. If the distance of the particle from O at time t be (a cos nt + b sin nt ) [ a,b and n are constants]., show that the acceleration of the particle varies as its distance from O. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEBook:CHHAYA PUBLICATIONChapter:SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEExercise:LONG ANSWER TYPE QUESTIONS
Explore 23 Videos
- SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEBook:CHHAYA PUBLICATIONChapter:SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEExercise:SAMPLE QUESTIONS FOR COMPETITVE EXAMINATION
Explore 20 Videos
- SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEBook:CHHAYA PUBLICATIONChapter:SIGNIFICANCE OF DERIVATIVE AS RATE OF CHANGEExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 19 Videos
- SET THEORY Book:CHHAYA PUBLICATIONChapter:SET THEORY Exercise:Assertion-Reason Type
Explore 2 Videos
- STRAIGHT LINE IN THREE DIMENSINAL SPACE Book:CHHAYA PUBLICATIONChapter:STRAIGHT LINE IN THREE DIMENSINAL SPACE Exercise:Sample Questions for Competitive Examination
Explore 19 Videos
Similar Questions
What do you mean by 'differential of a function? The radius of a sphere was found by measurement as 20 cm. if the maximum error in this measurement is 0.05 cm , find the maximum error that will occur. In the computation of the curved surface of the sphere.
View SolutionFind the points on the curve y=x2+1x2 at which dydx=0.
View SolutionFind the differential of each of the following functions
y =x3−3x2+2x
View SolutionLet A={1,2,3}andB={3,8}
Statement-I : (A∪B)×(A∩B)={(1,3),(2,3),(3,3),(8,3)}
Statement-II : (A×B)∩(B×A)={(3,3)}
View SolutionThe symmetrical from of the lines x+y+z−1=0 and 4x+y−2z+2=0 are -
View SolutionTwo particles, 1 and 2, move with constant velocities v_1 and v_2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l_1 and l_2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is

View SolutionA particle is moving on a straight line and its distance x cms from a fixed point O on the line is given byx=√t2+1 then the velocity of particle at t=1 is
View SolutionIf a particle moving in a straight line and its distance x cms from a fixed point O on the line is given by x=√1+t2 cms, then acceleration of the particle at t sec. is
View SolutionA particle is moving on a straight line so that its distance s from a fixed point at any time t is proportional to tn. If v be the velocity and 'a' the acceleration at any time , then nasn−1 equals
View SolutionThe distance form a fixed point O of a particle pmoving in a straight line from O is given by s=16+48t−t3. The direction of motion of the particle after t=4 sec is
View Solutionएक कण स्थिरावस्था से एक धनात्मक x-अक्ष की दिशा में मूल बिंदु O से नियत त्वरण से चलता है | वह सभी चित्र ज्ञात कीजिये जो इस कण की गति को गुणात्मक रूप से सही दर्शाते हैं (a = त्वरण, v = वेग, x = विस्थापन, t = समय)
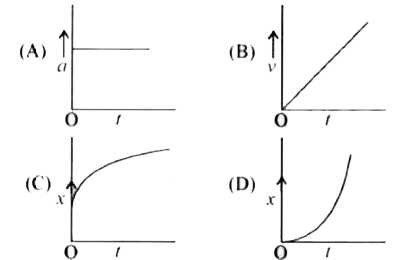
View Solutionএকটি কণা সরলরেখায় গতিশীল এবং O সরলরেখার ওপর একটি নির্দিষ্ট বিন্দু t সময়ে O বিন্দু থেকে দূরত্ব acosnt+bsinnt (a,b,n ধ্রুবক) হলে প্রমাণ করো যে কণার ত্বরণ O বিন্দু থেকে তার দূরত্বের সমানুপাতিক
View Solutionএকটি কণা সরলরেখায় গতিশীল এবং O সরলরেখার ওপর একটি নির্দিষ্ট বিন্দু। t সময়ে O বিন্দু থেকে কণার দূরত্ব acost+bsint (a,b ধুবক) হলে প্রমাণ করো যে, কণার ত্বরণ O বিন্দু থেকে তার দূরত্বের সমানুপাতিক।
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View Solution

