200 व्यक्ति किसी चर्म रोग से पीड़ित हैं जिनमें 120 व्यक्ति रसायन C1 से, 50 व्यक्ति रसायन C2 से तथा 30 व्यक्ति रसायन C1 और C2 दोनों से प्रभावित हैं । ऐसे व्यक्तियों की संख्या ज्ञात कीजिए जो
(i) रसायन C1 या C2 दोनों से प्रभावित हैं। ऐसे व्यक्तियों की संख्या ज्ञात कीजिए जो
(i) रसायन C1 या C2 से प्रभावित हैं।
(ii) रसायन C1 से प्रभावित हैं परंतु C2 से नहीं।
(iii) रसायन C2 से प्रभावित हैं परंतु C1 से नहीं।
यहां n(C1)=120,n(C2)=50,n(C1∩C2)=30
और n(U)=200
(i) n(C1∪C2)=n(C1)+n(C2)−n(C1∩C2)
=120+50−30=140
(ii) n(C1−C2)=n(C1)−n(C1∩C2)
=120−30=90
(iii) n(C2−C1)=n(C2)−n(C1∩C2)
=50−30=20
Topper's Solved these Questions
- समुच्चयBook:NOOTAN HINDIChapter:समुच्चयExercise:प्रश्नावली 1 A
Explore 7 Videos
- समुच्चयBook:NOOTAN HINDIChapter:समुच्चयExercise:प्रश्नावली 1 B
Explore 10 Videos
- शंकु परिच्छेदBook:NOOTAN HINDIChapter:शंकु परिच्छेदExercise:प्रश्नावली 11G (विविध प्रतियोगी परीक्षाओं हेतु प्रश्न)
Explore 10 Videos
- सम्बन्ध एवं फलनBook:NOOTAN HINDIChapter:सम्बन्ध एवं फलनExercise:प्रश्नावली ( विविध प्रश्नावली )
Explore 12 Videos
Similar Questions
यदि A={1,2,3,4,5,6} तो रिक्त स्थानों मे ∈ या ∉ भरिए
(i) 2…………….A (ii) 7…………….A
(iii) 0……………..A (iv) 5……………….A
View Solutionनिम्नलिखित में से कौन- से रिक्त समुच्चय के उदाहरण हैं?
(i) {x:xεN,x<9 और x>9} ltbrLgt (ii) {x:x दो लम्बवत रेखाओं का उभयनिष्ठ बिंदु है}
(iii) 3 से विभाजय सम प्राकृतिक संख्याओं का समुच्चय
(iv){x:x2=4,x एक विषम संख्या है}
View SolutionP(α,β) से होकर जाने वाली एक सरल रेखा , वृत्त को बिन्दुओ A और B पर काटती है| PA . PB का मान है -
View Solutionसम्बन्ध f,f(x)={x2,0≤x≤33x,3≤x≤10 द्वारा परिभाषित है ।
सम्बन्ध g,g(x)={x2,0≤x≤23x,2≤x≤10 द्वारा परिभाषित है ।
दर्शाइए कि क्यों f एक फलन है और g फलन नहीं है ।
View SolutionC_(0)C_(1)+C_(1)C_(2)+C_(2)C_(3)+...+C_(n-1)C_(n)
View SolutionProve that (C_(0)+C_(1))(C_(1)+C_(2))(C_(2)+C_(3))(C_(n-1)+C_(n))=((n+1)^(n))/(n!)*c_(0)*C_(1)*C_(2).........
View SolutionIf (1+x+x^(2))^(n)=(C_(0)+C_(1)x+C_(2)x^(2)+.........) then the value of C_(0)C_(1)-C_(1)C_(2)+C_(2)C_(3)...
View SolutionIn C_(0),C_(1)C_(2)….C_(n) are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
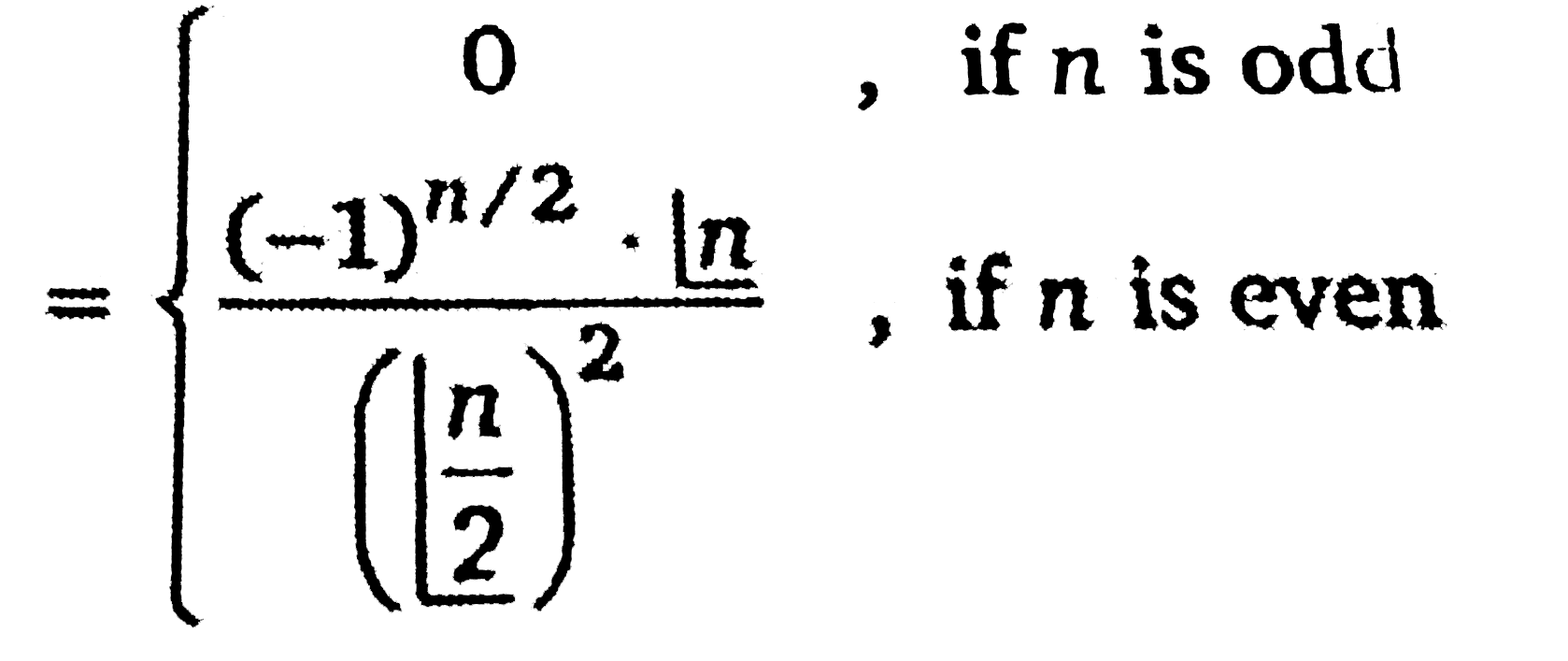
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
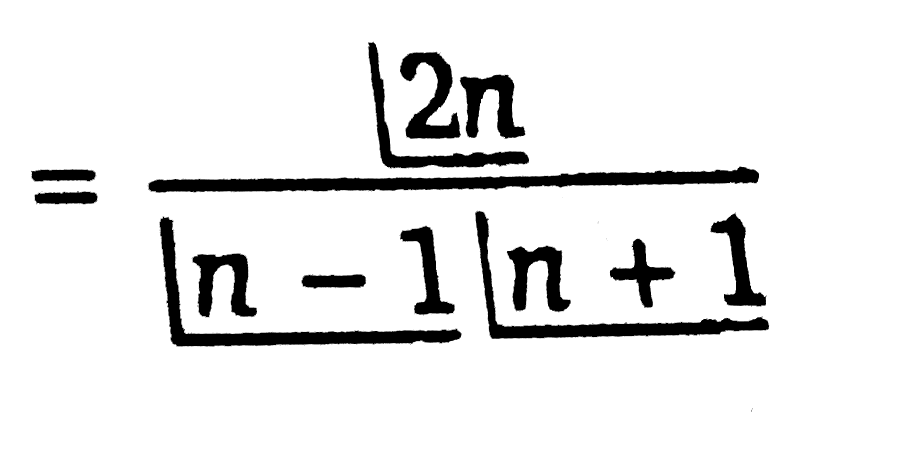
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
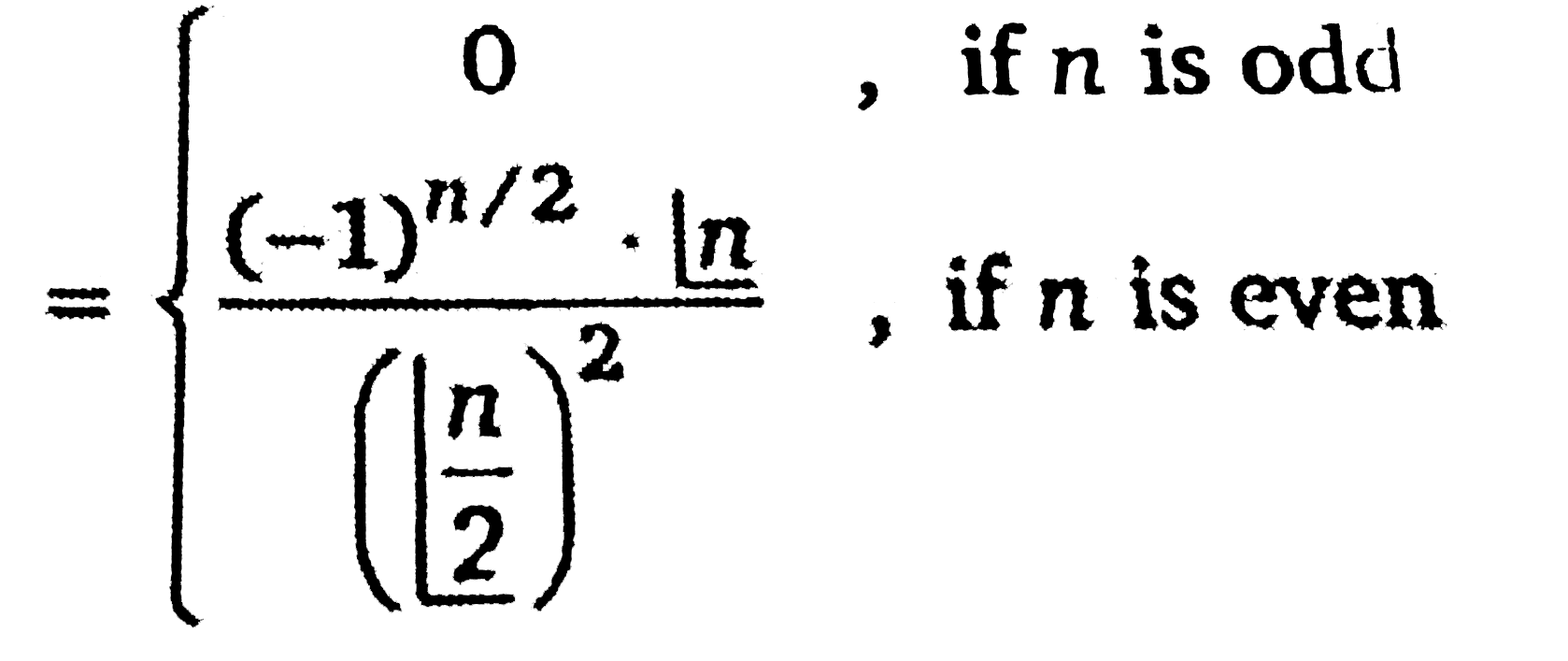
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
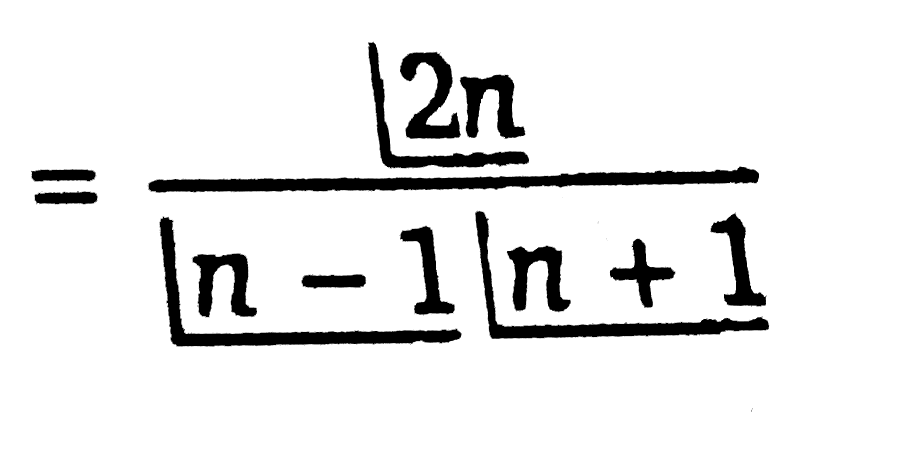
View Solution(C0+C1)(C1+C2)(C2+C3)....(Cn−1+Cn)=
View Solutionनिम्नलिखित में से किसी एक शब्द का विशेषण रूप लिखिए :
(अ) रसायन | (ब) पुराण|
View Solutionउचित प्रत्यय लगाकर निम्नलिखित में से किसी एक शब्द का विशेषण रूप लिखिए
रसायन
View Solutionउस अवकल समीकरण की कोटि जिसका व्यापक हल y=c1e2x+c2+c3ex+c4sin(x+c5) है, हैं
View SolutionIf (1+x+x2)n=c0+c1x+c2x2+…., then the value of c0c1−c1c2+c2c3−…… is
View Solutionएक संधारित्र C1=4μF तथा एक - दूसरे संधारित्र C2=1μF को श्रेणीक्रम संयोजन के साथ जोड़ा गया हैं | इसी संयोजन में 2000 की बैटरी जोड़ दी जाये तो C2 से C1 के बीच का विभव का अनुपात है |
View Solutionयदि (1+x)n=C0+C1x+C2x2+....+Cnxn तब C0−(C0+C1)+(C0+C1+C2)−(C0+C1+C2+C3) जहाँ n रागपूर्णांक है
View Solution

