Question

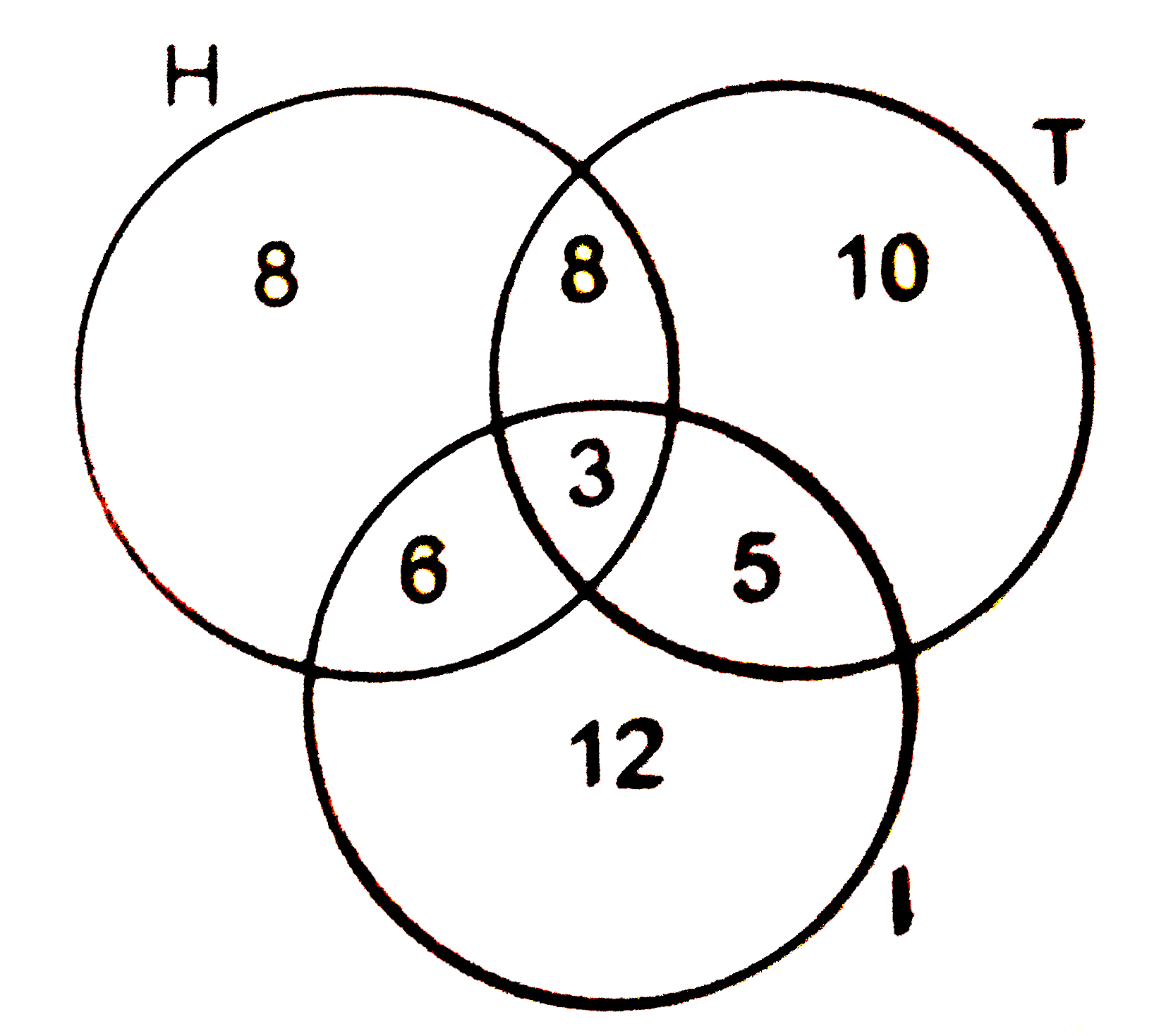
60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समावचार पत्र $H$, 26 लोग समाचार -पत्र T, 26 लोग समाचार –पत्र I,9 लोग $H$ तथा $I$ दोनों, 11 लोग $H$ तथा $T$ दोनों,8 लोग $T$ तथा $I$ दोनों और 3 लोग तीनों ही समाचार पत्र पढ़ते हैं तो निम्नलिखित ज्ञात कीजिएः
(i) कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
(ii) ठीक-ठीक केवल एक समाचार पत्र पढ़ने वालों की संख्या।

Explanation

माना समाचार पत्र `H` पढ़ने वाले लोगों की संख्या `n(H),` समाचार –पत्र `T` पढ़ने वाले लोगों की संख्या `n(T)` और समाचार –पत्र `I` पढ़ने वाले लोगों की सख्ंया `n(I)` है।
`:.n(H)=25,n(T)=26,n(I)=26`
`n(HnnT)=11,n(TnnI)=8,n(HnnI)=9`
तथा `n(HnnTnnI)=3`
(i) कम से कम एक समाचार पत्र पढ़ने वाले लोगों की संख्‍या `n(HuuTuuI)` होगी।
तब `n(HuuTuuI)=n(H)+n(T)+n(I)-n(HnnT)`
`-n(TnnI)-n(HnnI)+n(HnnTnnI)`
`=25+26+26-11-8-9+3=52`
अतः 52 लोग कम से कम एक समाचार पत्र अवश्य पढ़ते है।
(ii) `:.` केवल H व T समाचार –पत्र पढ़ने वालों की संख्या
`=n(HnnT)-n(HnnTnnI)`
`=11-3=8`
इसी प्रकार केवल T व I समाचार पत्र पढ़ने वालों की संख्या

`=n(TnnI)-n(HnnTnnI)=8-3=5`
और केवल H व I समाचार – पत्र पढ़ने वालों की संख्या
`=n(HnnI)-n(HnnTnnI)=9-3=6`
अतः केवल दो समाचार पत्र पढ़ने वालों की संख्या
`=8+5+6=19`
उनमें तीनों समाचार –पत्र पढ़ने वाले सम्‍मिलित नहीं हैं।
अतः कम से कम दो समाचार पत्र पढ़ने वालों की कुल संख्या
`=` दो `+` तीन समाचार पत्र पढ़ने वालों की संख्या
`=19+3=22`
`:.` केवल एक समाचार पत्र पढ़ने वालों की संख्या
`=52-22=30`
अतः 30 लोग केवल एक समाचार पत्र पढ़ते हैं।