AB एक रेखाखण्ड है और P इसका मध्य- बिन्दु है। D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार है कि ∠BAD=∠ABE और ∠EPA=∠DPB
है (देखिए आकृति)। दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD=BE

(i) ∠APE=∠BPD (दिया है)
⇒∠APE+∠EPD=∠BPD+∠EPD
⇒∠APD=∠BPE
ΔDAP और ΔEBP में,
∠APD=∠BPE (सिद्ध क्र चुके है )
AP=BP (P,AB का माध्य-बिन्दु है)
∠PAD=∠PBE
(∵∠BAD=∠ABE दिया है )
∴ΔDAP≅ΔEBP (A.S.A.)
(ii) AD=BE (c.p.c.t.)
Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7.2
Explore 8 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7.3
Explore 5 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7B
Explore 19 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- दो चरों वाले रैखिक समीकरण Book:NOOTAN HINDIChapter:दो चरों वाले रैखिक समीकरण Exercise:विविध प्रश्नावली
Explore 12 Videos
Similar Questions
एक समद्विबाहु त्रिभुज ABC में, जिसमे AB = AC है, ∠A और ∠C के समद्विभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते है। A और O को जोड़िए। दर्शाइए कि
(i) OB= OC
(ii) AO कोण A को समद्विभाजित करता है।
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP, कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

View SolutionΔABC में, AB=8 सेमी, BC = 15 सेमी और AC = 17 सेमी है। सबसे कोण ज्ञात कीजिए।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionMatch the following Column A to Column B

View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
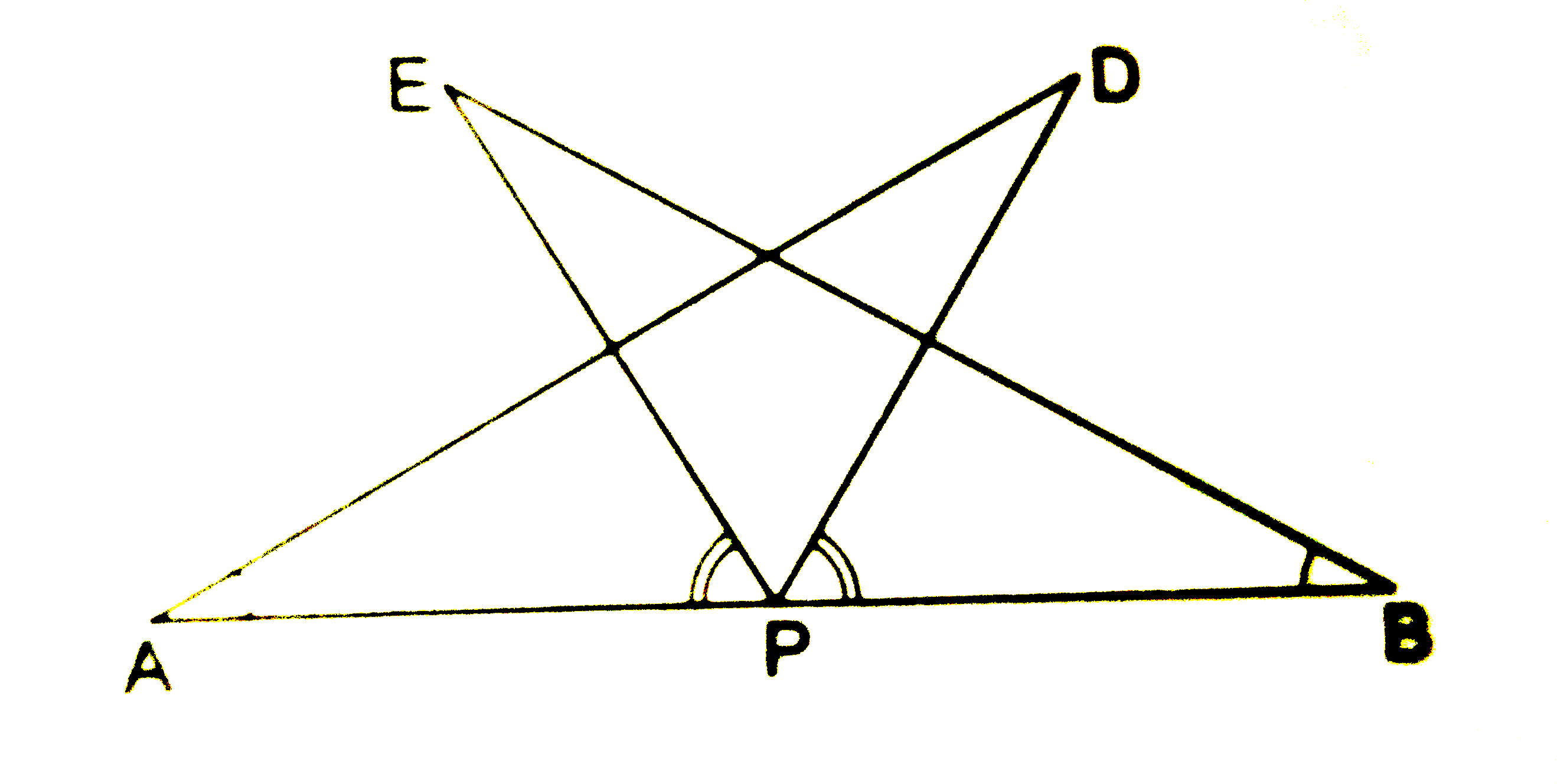
View SolutionAB एक रेखाखंड है और P इसका मध्य बिंदु है | D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD=∠ABE और ∠EPA=∠DPB है | (देखिए चित्र) | दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD = BE
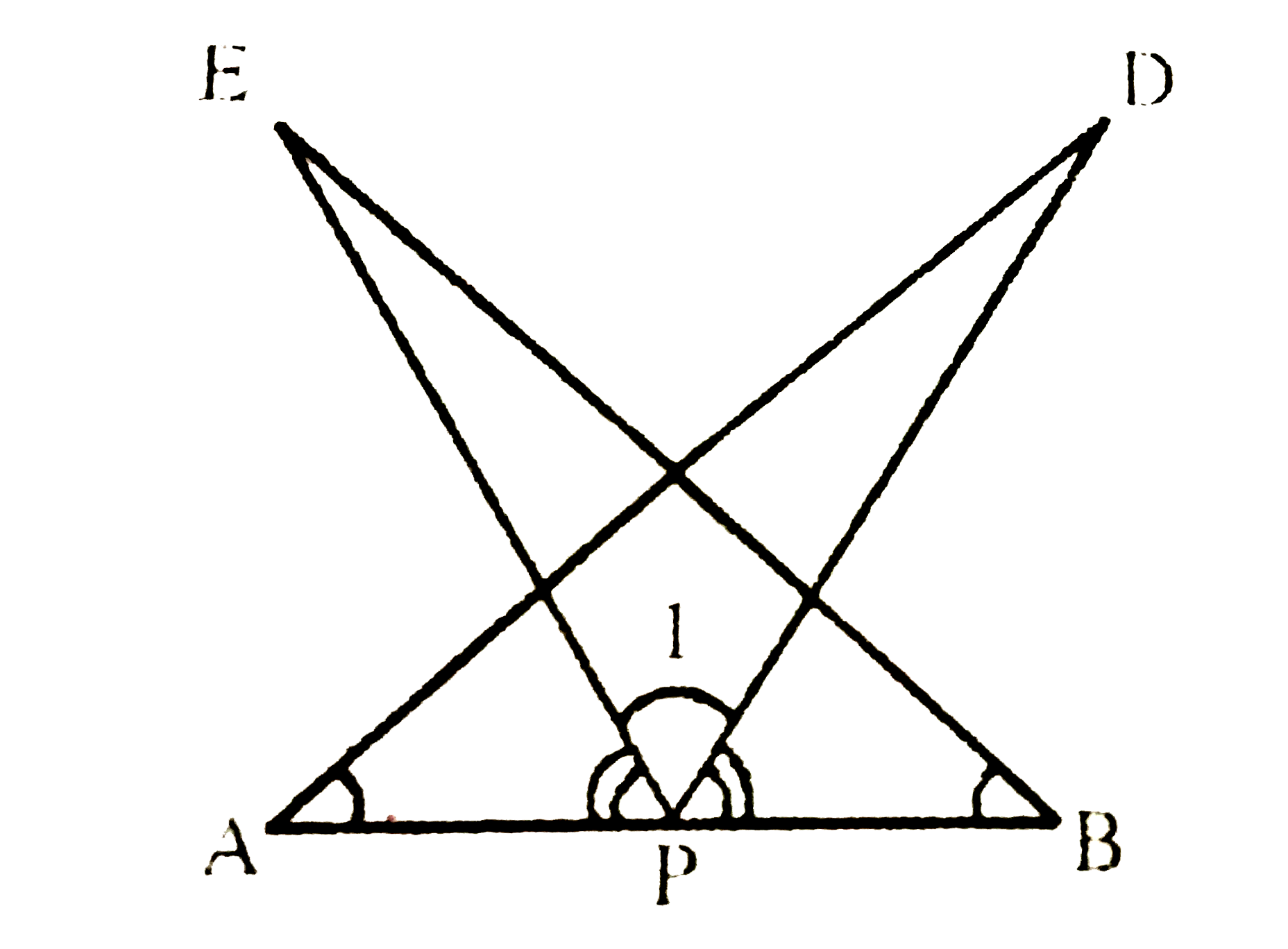
View SolutionAB एक रेखाखण्ड है तथा P इसका मध्यबिंदु है और AB की समान भुजा पर बिंदु D व E इस प्रकार है कि ∠BAD=∠ABE तथा ∠EPA=∠DPB तो सिद्ध कीजिए कि : ΔDAP≅ΔEBP
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solution

