AB एक रेखाखंड है और P इसका मध्य बिंदु है | D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD=∠ABE और ∠EPA=∠DPB है | (देखिए चित्र) | दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD = BE
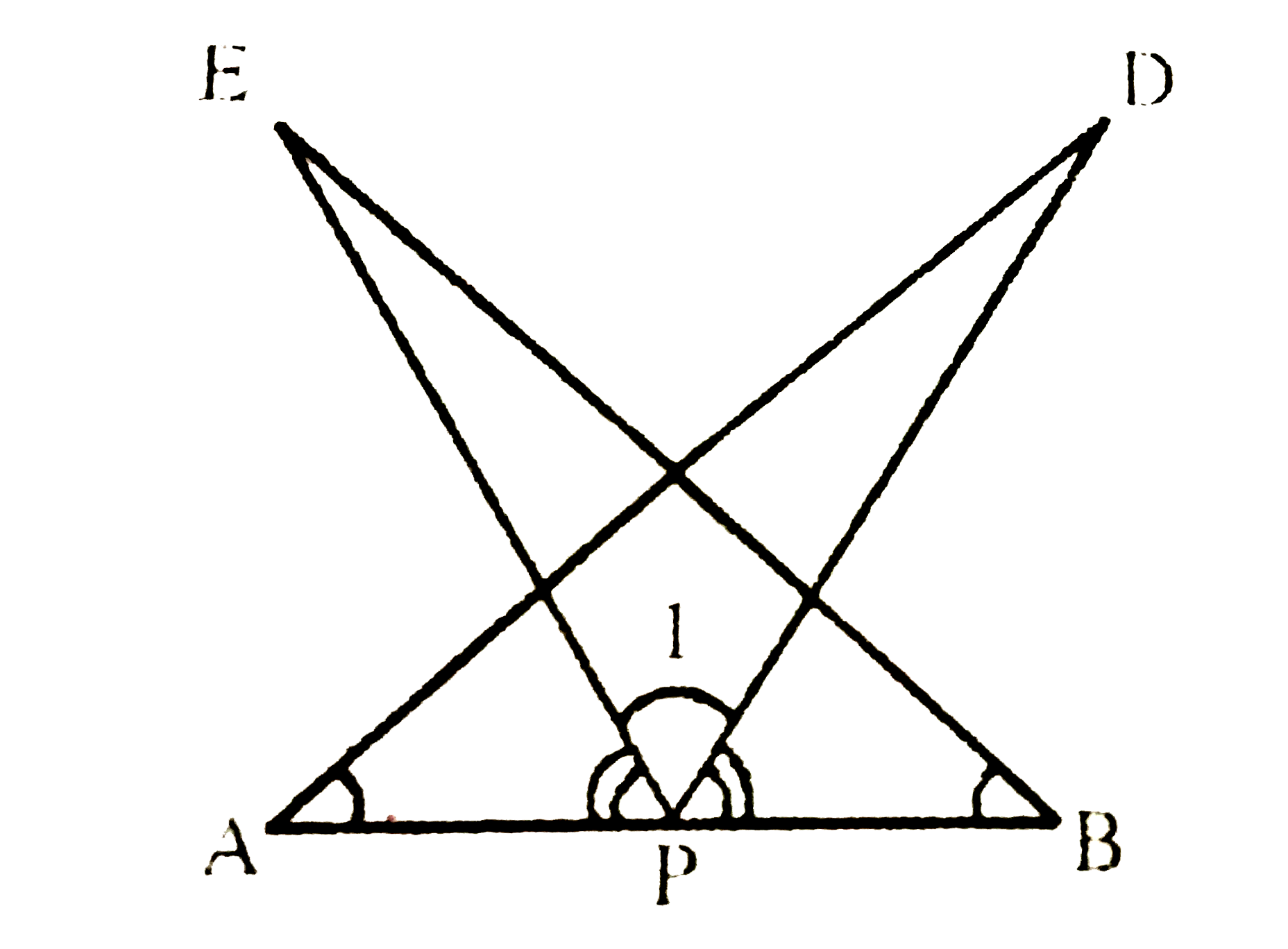
ΔDAP तथा ΔEBP में,
AP=BP [∵C, AB का मध्य बिन्दु है]
∠PAD=∠PBE [दिया है]
∠APD=∠APE+∠1
=∠BPD+∠1 [∵∠APE=∠BPD]
=∠BPE
इस प्रकार ΔDAP≅ΔEBP [ASA कसौटी से]
अत: DA=EB [CPCT]

Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता Book:KC SINHAChapter:त्रिभुजों की सर्वांगसमता Exercise:अभ्यास 9.1 (अतिलघु उत्तरीय प्रश्न )
Explore 36 Videos
- त्रिभुजों की सर्वांगसमता Book:KC SINHAChapter:त्रिभुजों की सर्वांगसमता Exercise:अभ्यास 9.1 लघु उत्तरीय प्रश्न
Explore 11 Videos
- ज्यामितीय बनावट ( रचनाएँ ) Book:KC SINHAChapter:ज्यामितीय बनावट ( रचनाएँ ) Exercise:उदाहरण
Explore 11 Videos
- दो चरों वाले रैखिक समीकरण Book:KC SINHAChapter:दो चरों वाले रैखिक समीकरण Exercise:वस्तुनिष्ट प्रश्न
Explore 15 Videos
Similar Questions
यदि किसी त्रिभुज की दो भुजाएँ और उनके .............. कोण, दूसरे त्रिभुज की तदनुरूपी दोनों भुजाओं तथा उनके अंतर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं |
View Solutionदो त्रिभुजों के सर्वांगसम होने के लिए भुजा-भुजा-भुजा प्रतिबंध को लिखें |
View Solutionएक △ABC बनाये जिसमे BC या (a) =6.6सेमि, CA+AB या (b+c) =10.2 सेमि तथा ∠B=60∘
View Solutionएकघातीय समीकरण ax+by+c=0 के वास्तविक हलो की संख्या है
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
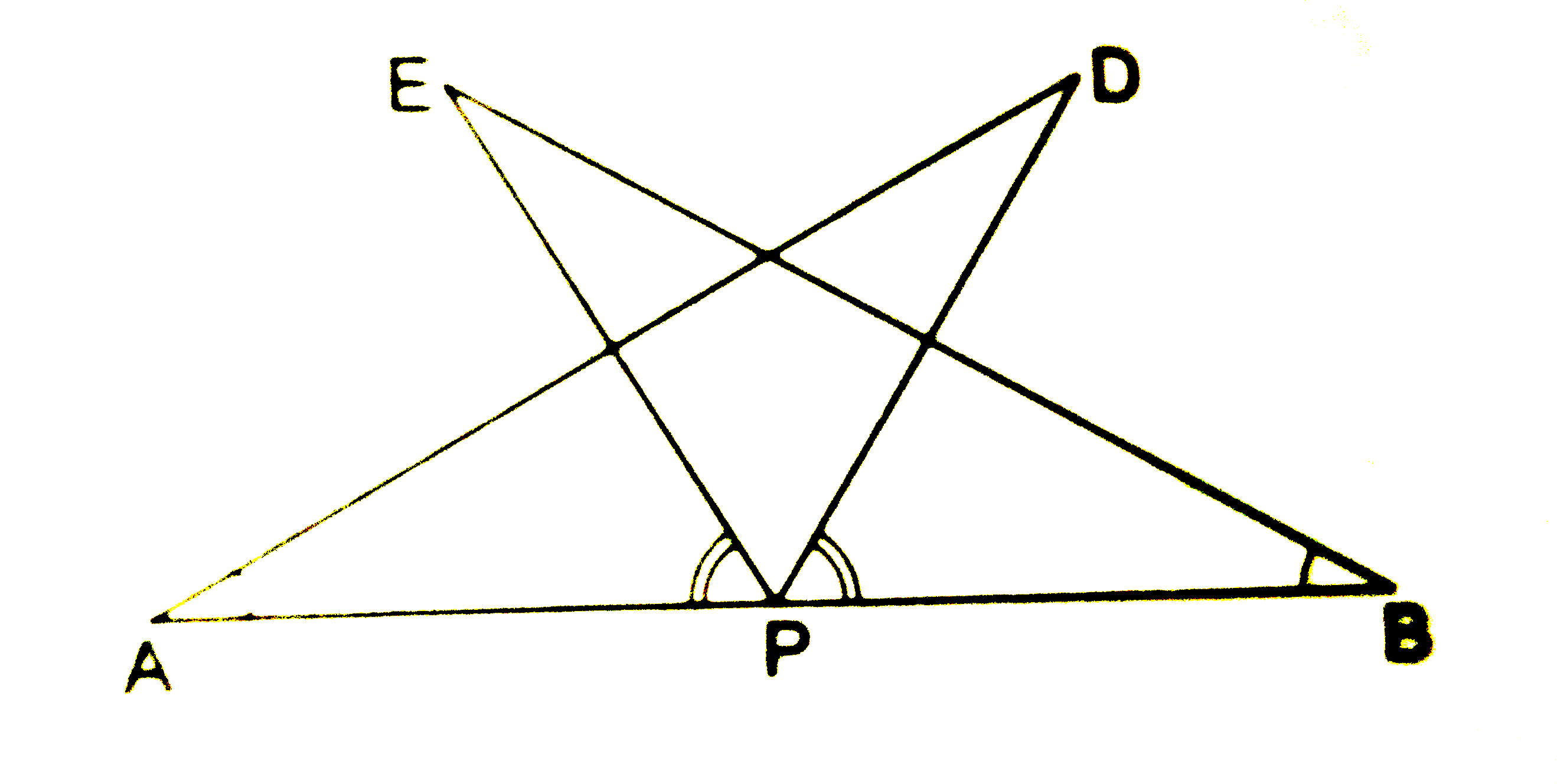
View SolutionAB एक रेखाखण्ड है तथा P इसका मध्यबिंदु है और AB की समान भुजा पर बिंदु D व E इस प्रकार है कि ∠BAD=∠ABE तथा ∠EPA=∠DPB तो सिद्ध कीजिए कि : ΔDAP≅ΔEBP
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View SolutionAB एक रेखाखण्ड है और P इसका लम्ब-बिन्दु है | D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार है कि ∠BAD -= ∠ABE और ∠EPA -= ∠DPB है | ( देखिए आकृति ) दर्शाइए कि-
(i) ΔDAP ~-= ΔEBP
(ii) AD -= BE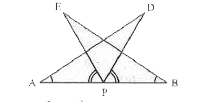
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AP such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.

View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution

