20 सेमी ऊंचाई और शीर्ष कोण (vertical angle ) $60^{\circ}$ वाले एक शंकु को उसकी ऊंचाई के बीचों - बीच से होकर जाते हुए एक ताल से दो भागों में काटा गया है , जबकि ताल शंकु के आधार के समांतर है । यदि इस प्राप्त शंकु के छिन्नक को व्यास $\frac{1}{16}$ सेमी वाले एक तार के रूप में बदल दिया जाता है तो तार की लम्बाई ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

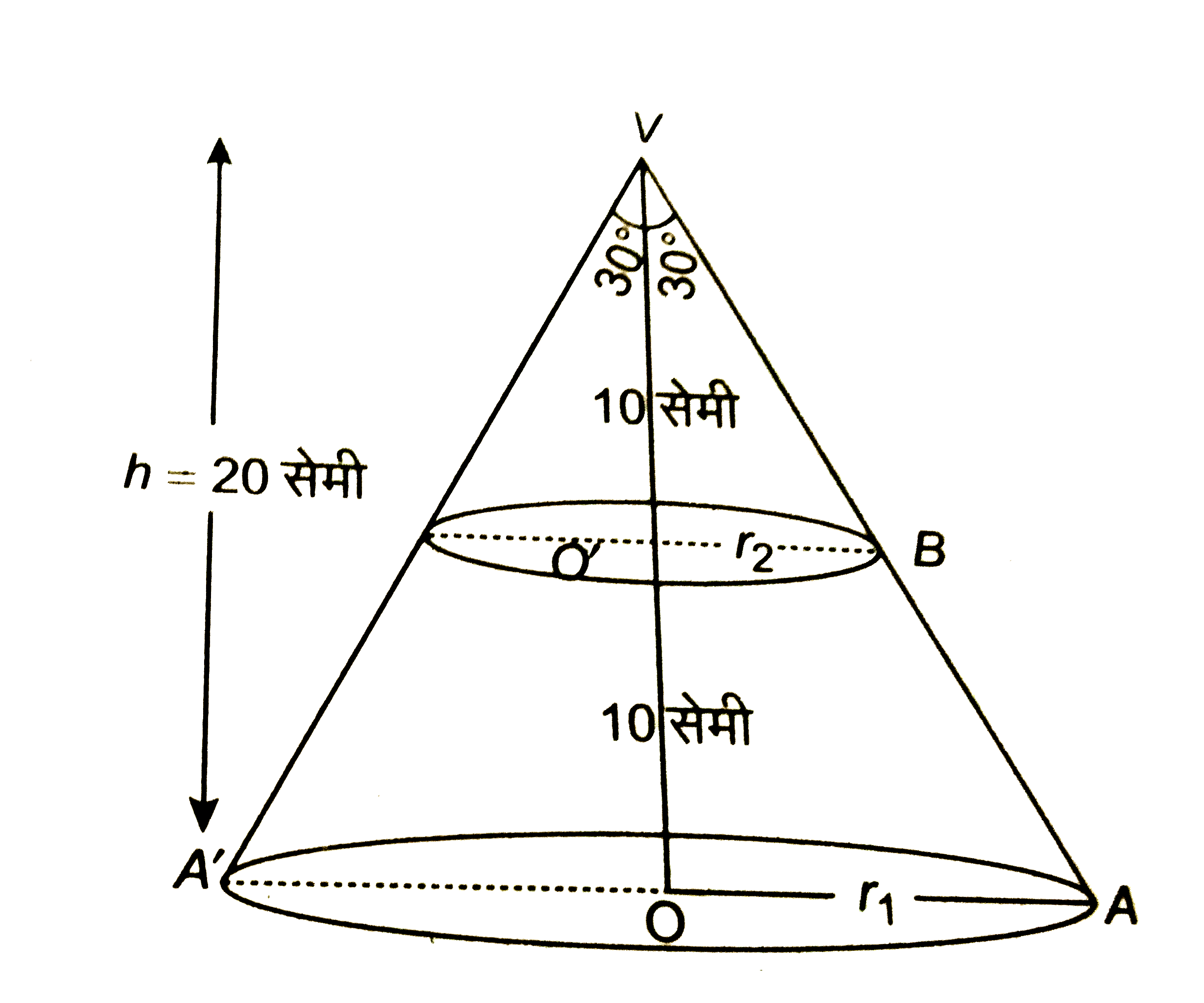
चित्र में किसी शंकु के आधार का व्यास A'OA है तथा शीर्ष V है । शंकु का शीर्ष कोण $A' V A = 60^{\circ}$ है , तब शंकु का अर्द्धशीर्ष कोण $α = 30^{\circ}$
शंकु की ऊंचाई सेमी $= 20$ है ।
तब , समकोण $Δ O A V$ में ,
$tan α = \frac{O A}{O V} \Rightarrow n {tan 30}^{\circ} = \frac{r_{1}}{20} \Rightarrow \frac{1}{\sqrt{3}} = \frac{r_{1}}{20}$
$= r_{1} = \frac{20}{\sqrt{3}}$ सेमी
$∵ Δ V O B$ तथा $Δ V O A$ समरूप है ,
$∴ \frac{V O}{V O} = \frac{O' B}{O A} \Rightarrow \frac{10}{20} = \frac{r_{2}}{r_{1}} = \frac{r_{2}}{r_{1}} = \frac{1}{2}$

$\Rightarrow r_{1} = 2 r_{2} \Rightarrow r_{2} = \frac{1}{2} r_{1} = \frac{1}{2} \times \frac{20}{\sqrt{3}} = \frac{10}{\sqrt{3}}$ सेमी ।
और छिन्नक की ऊंचाई $h = \frac{1}{2} \times$ शंकु की ऊंचाई $= 10$ सेमी
तब छिन्नक का आयतन $= \frac{1}{3} π r (r_{1}^{2} + r_{1} r_{1} + r_{2}^{2}) = \frac{1}{3} π (10) ⎡ ⎣ {(\frac{20}{\sqrt{3}})}^{2} + \frac{20}{\sqrt{3}} \times \frac{10}{\sqrt{3}} + {(\frac{10}{\sqrt{3}})}^{2} ⎤ ⎦$
$= \frac{1}{3} π 10 [\frac{400}{3} + \frac{200}{3} + \frac{100}{3}]$
$= \frac{7000}{9} π$ घन सेमी
बेलनाकार तार का व्यास $= \frac{1}{16}$ सेमी
$\Rightarrow$ तार की त्रिज्या $r = - \frac{1}{32}$ सेमी
माना खींचे जाने वाले तार की लम्बाई l सेमी है ।
तब , तार का आयतन $= π r^{2} l$
$= π \times \frac{1}{32} \times \frac{1}{32} \times l = \frac{π}{1024} l$ घन सेमी
$∵$ तार , शंकु के छिन्नक से खींचा जाता है ।
$∴$ तार का आयतन = छिन्नक आयतन
$\Rightarrow \frac{π}{1024} l = \frac{7000}{9} π$
$\Rightarrow l = \frac{7000 π}{9} \times \frac{1024}{π}$ सेमी
$= \frac{70}{9} \times 1024)$ मीटर
$= \frac{71680}{9}$ मीटर
$= 7964.44$ मीटर
अतः तार की लम्बाई $= 7964.44$ मीटर ।

Updated on:21/07/2023

|

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-पृष्ठीय क्षेत्रफल और आयतन -ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.4)

Home
Ask Doubt
Profile