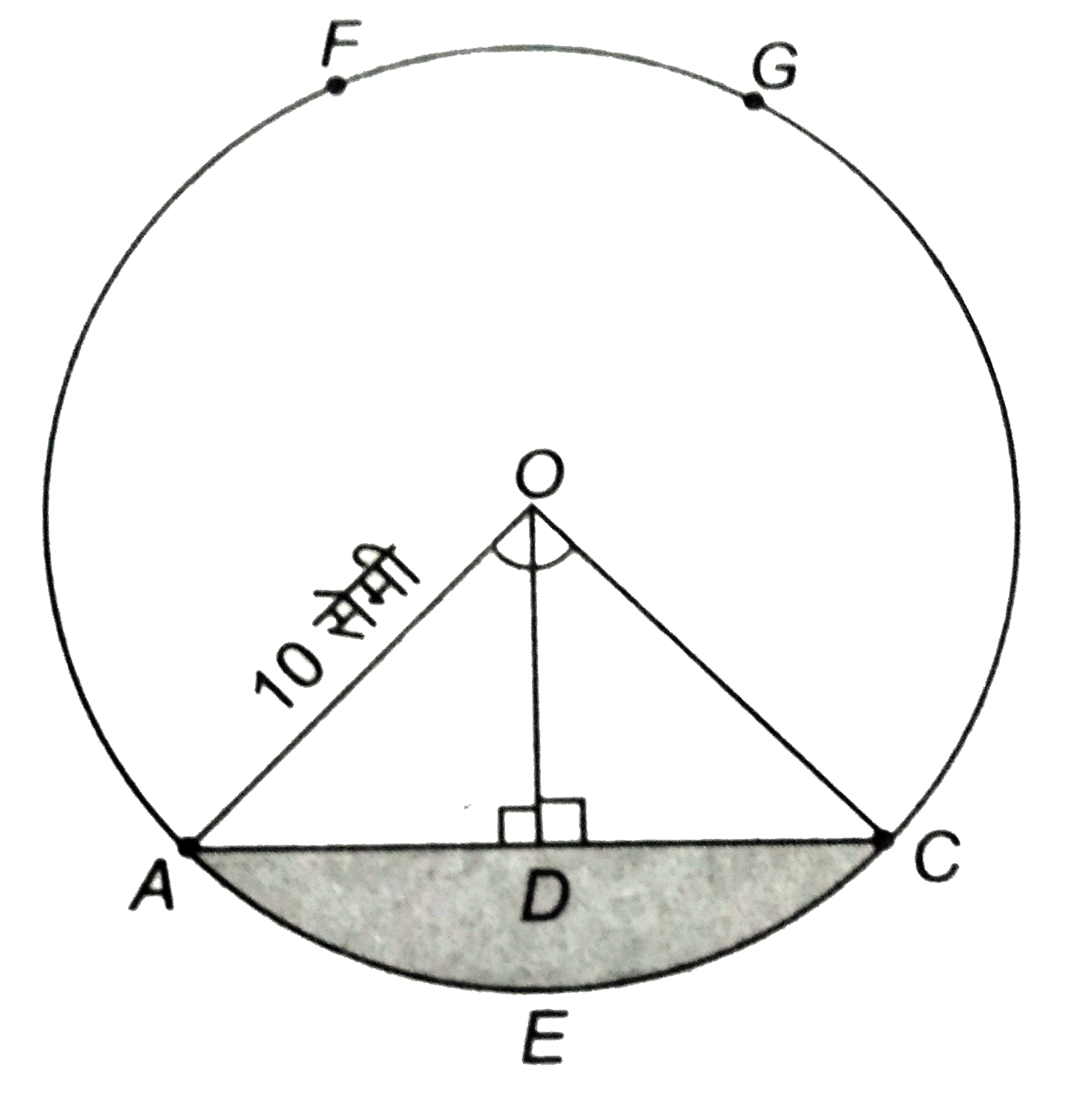
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है । निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) संगत लघु वृत्तखंड
(ii) संगत दीर्घ त्रिज्यखंड ( का प्रयोग कीजिए )।
दिया है , वृत्त की त्रिज्या
AO = 10 सेमी
वृत्त के केंद्र से वृत्त के जीवा पर लम्ब खींचा गया है , जो इस जीवा को समद्विभाजित करता है
तथा
समकोण में ,
सेमी
और
सेमी
अब , AC = 2AD
सेमी
अब , का क्षेत्रफल
=
अब त्रिज्यखण्ड का क्षेत्रफल
(i) लघु वृत्तखण्ड AEC का क्षेत्रफल = त्रिज्यखण्ड OAEC का क्षेत्रफल - AOC का क्षेत्रफल
(ii) दीर्घ त्रिज्यखण्ड OAFGCO का क्षेत्रफल = वृत्त का क्षेत्रफल - त्रिज्यखण्ड OAEC का क्षेत्रफल
Topper's Solved these Questions
- वृत्तों से समबन्धित क्षेत्रफल Book:NOOTAN HINDIChapter:वृत्तों से समबन्धित क्षेत्रफल Exercise:प्रश्नावली 12.3 (एनo सीo ईo आरo टीo प्रश्न )
Explore 32 Videos
- वृत्तों से समबन्धित क्षेत्रफल Book:NOOTAN HINDIChapter:वृत्तों से समबन्धित क्षेत्रफल Exercise:विविध प्रश्नावली ( अतिलघु उत्तरीय प्रश्न )
Explore 24 Videos
- वृत्तों से समबन्धित क्षेत्रफल Book:NOOTAN HINDIChapter:वृत्तों से समबन्धित क्षेत्रफल Exercise:प्रश्नावली 12.1 (एनo सीo ईo आरo टीo प्रश्न )
Explore 10 Videos
- वृत्त Book:NOOTAN HINDIChapter:वृत्त Exercise:बहुविकल्पीय प्रश्न
Explore 7 Videos
- समान्तर श्रेढ़ी Book:NOOTAN HINDIChapter:समान्तर श्रेढ़ी Exercise:विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )
Explore 7 Videos
Similar Questions
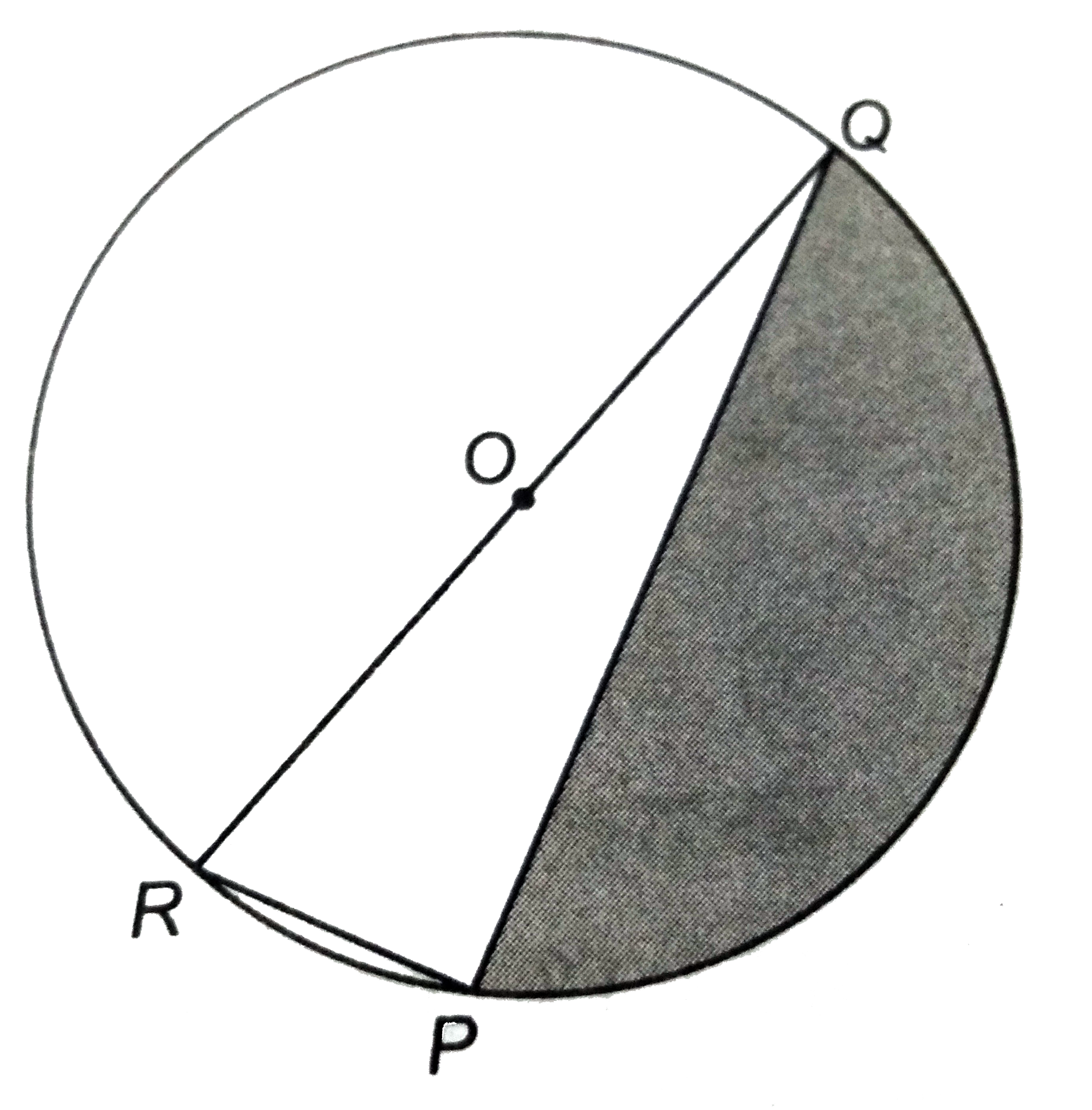
आकृति में , छायांकित भाग का क्षेत्रफल ज्ञात कीजिए , यदि PQ = 24 सेमी , PR = 7 सेमी तथा O वृत्त का केंद्र है ।
View Solutionएक वृत्त की त्रिज्या 7 सेमी है । इसका क्षेत्रफल ज्ञात कीजिए ।
View Solutionदो वृत्तों की त्रिज्याएँ क्रमश : 19 सेमी और 9 सेमी है । उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है ।
View Solutionयदि वृत्त की दो त्रिज्याओं के बीच का कोण 110∘ हो, तो इन त्रिज्याओं के सिरों पर खींची गई स्पर्श रेखाओं के बीच का कोण है :
View Solution3 के प्रथम 6 गुणांकों का योग है:
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionएक2.7 सेमी त्रिज्या लेकर वृत्त की रचना कीजिए। उस वृत्त पर एक स्पर्श रेखा खींचिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionA circle is drawn circumscribing a rectangle of sides 24 cm and 7 cm. Find the area of the circle. (Take pi=3.14 ) एक वृत्त 24 cm और 7 cm भुजा वाले आयत के परिगत है। वृत्त का क्षेत्रफल ज्ञात कीजिए।( pi=3.14 )
View SolutionA chord of length 24 cm is at a distance of 5 cm from the centre of a circle. What is its area? एक वृत्त के केंद्र से 5 सेमी की दूरी पर 24 सेमी लंबाई का एक जीवा है। इसका क्षेत्रफल क्या है?
View Solution