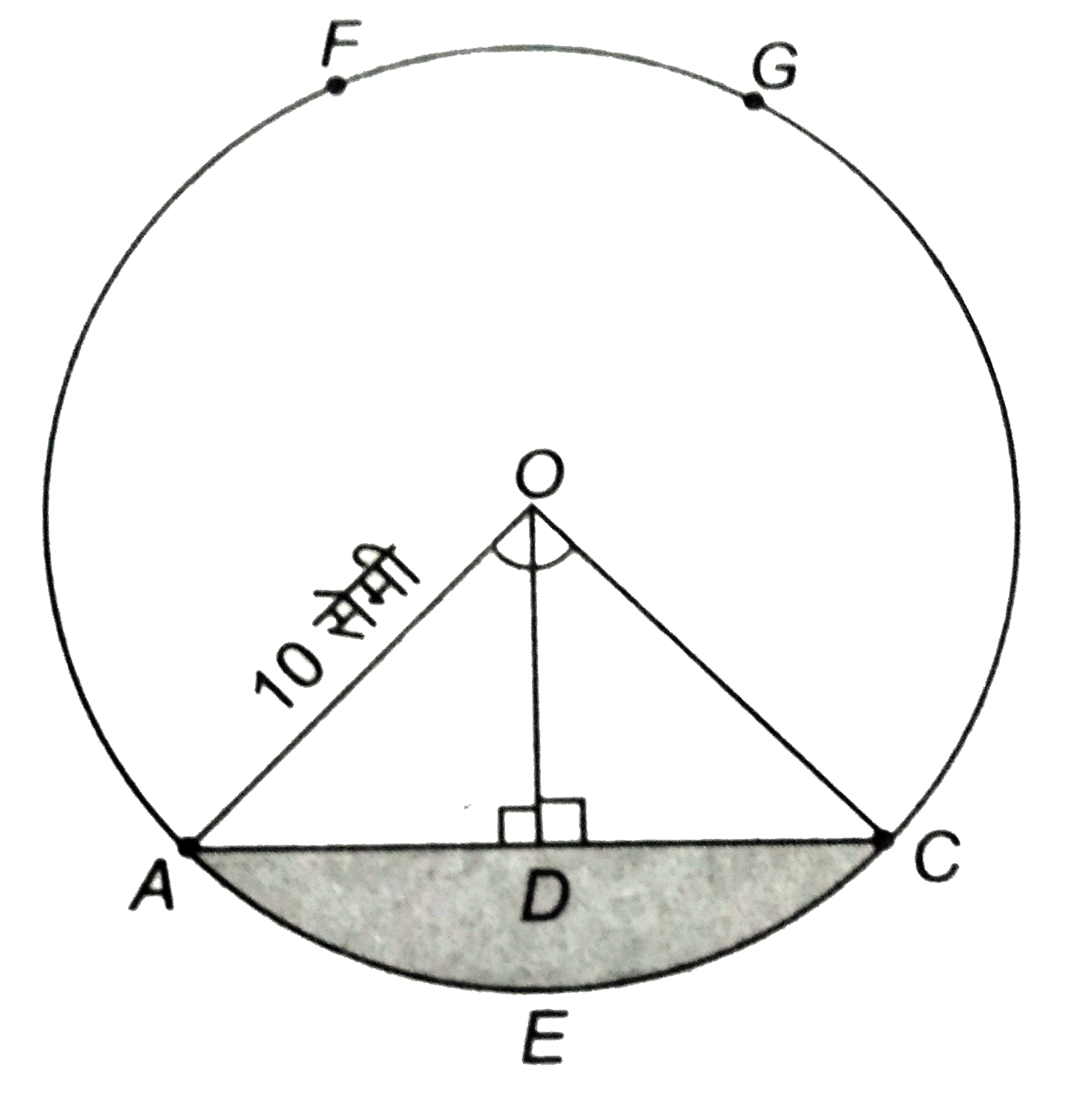
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है । निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) संगत लघु वृत्तखंड
(ii) संगत दीर्घ त्रिज्यखंड (π=3.14 का प्रयोग कीजिए )।
दिया है , वृत्त की त्रिज्या
AO = 10 सेमी
वृत्त के केंद्र से वृत्त के जीवा पर लम्ब खींचा गया है , जो इस जीवा को समद्विभाजित करता है
∴AD=DC
तथा ∠AOD=∠COD=45∘
∴∠AOC=∠AOD+∠COD
=45∘+45∘=90∘
समकोण ΔAOD में ,
⇒sin45∘=ADAO⇒1√2=AD10
AD=5√2 सेमी
और cos45∘=ODAO⇒1√2=OD10
⇒OD=5√2 सेमी
अब , AC = 2AD
=2×5√2=10√2 सेमी
अब , ΔAOC का क्षेत्रफल
=12AC×OD
= 12×10√2×5√2=50सेमी 2
अब त्रिज्यखण्ड का क्षेत्रफल
θπr2360∘=90∘360∘×3.14×(10)2
=3144=78.5सेमी 2
(i) ∴ लघु वृत्तखण्ड AEC का क्षेत्रफल = त्रिज्यखण्ड OAEC का क्षेत्रफल - AOC का क्षेत्रफल
=78.5−50=28.5 सेमी2
(ii) ∴ दीर्घ त्रिज्यखण्ड OAFGCO का क्षेत्रफल = वृत्त का क्षेत्रफल - त्रिज्यखण्ड OAEC का क्षेत्रफल
=πr2−78.5=3.14×(10)2−78.5
=314−78.5=235.5सेमी 2
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - प्रश्नावली 12.3 (एनo सीo ईo आरo टीo प्रश्न )32videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( अतिलघु उत्तरीय प्रश्न )24videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - प्रश्नावली 12.1 (एनo सीo ईo आरo टीo प्रश्न )10videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - बहुविकल्पीय प्रश्न7videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )7videos
समान्तर श्रेढ़ी
Similar Questions
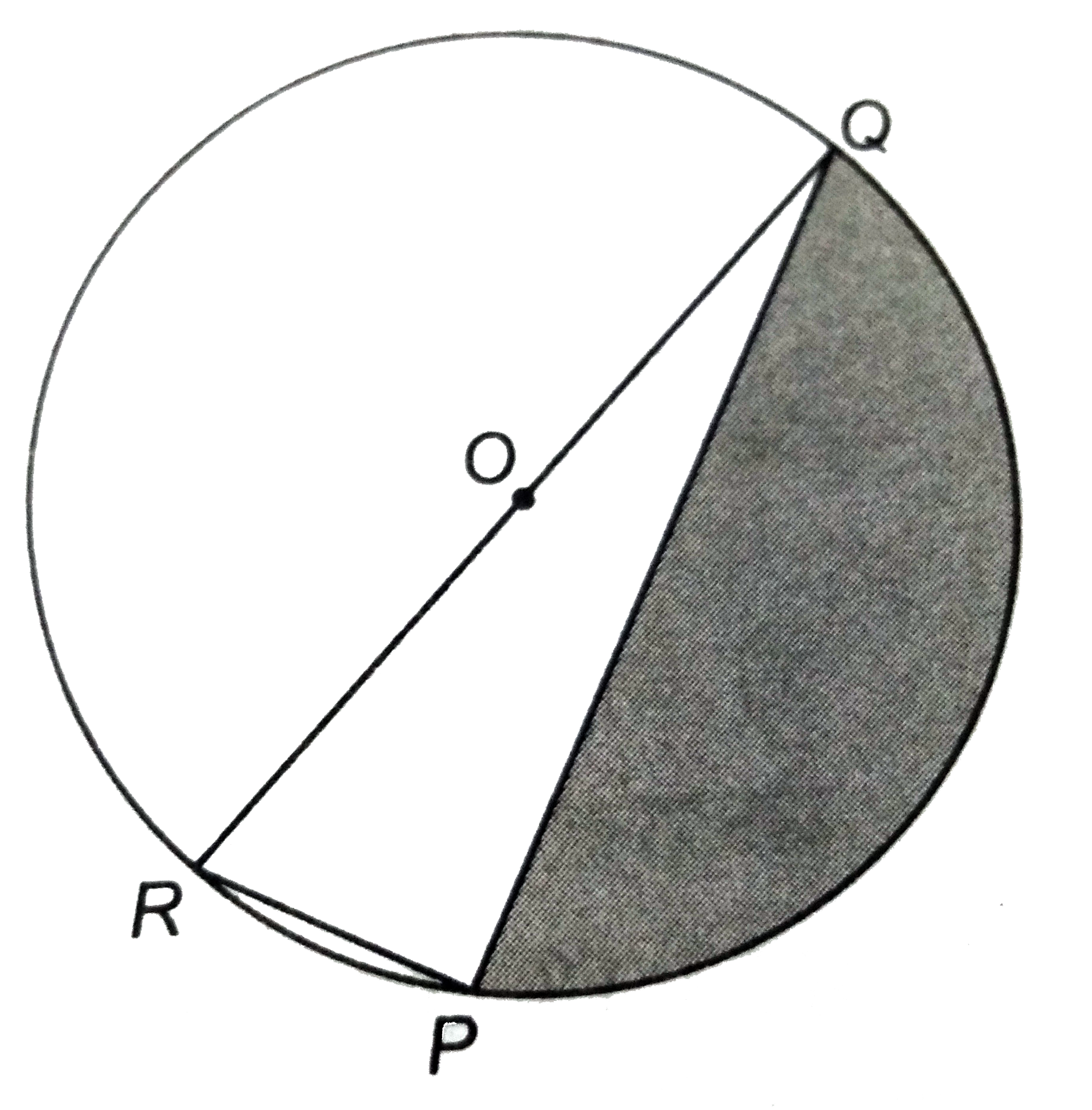
आकृति में , छायांकित भाग का क्षेत्रफल ज्ञात कीजिए , यदि PQ = 24 सेमी , PR = 7 सेमी तथा O वृत्त का केंद्र है ।
 02:20View Solution
02:20View Solutionएक वृत्त की त्रिज्या 7 सेमी है । इसका क्षेत्रफल ज्ञात कीजिए ।
00:59View Solutionदो वृत्तों की त्रिज्याएँ क्रमश : 19 सेमी और 9 सेमी है । उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है ।
01:25View Solutionयदि वृत्त की दो त्रिज्याओं के बीच का कोण 110∘ हो, तो इन त्रिज्याओं के सिरों पर खींची गई स्पर्श रेखाओं के बीच का कोण है :
05:33View Solution3 के प्रथम 6 गुणांकों का योग है:
03:41View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
02:01View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
02:30View Solutionएक2.7 सेमी त्रिज्या लेकर वृत्त की रचना कीजिए। उस वृत्त पर एक स्पर्श रेखा खींचिए।
02:27View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
02:52View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
03:14View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
02:28View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
02:05View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
01:21View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
01:48View SolutionA circle is drawn circumscribing a rectangle of sides 24 cm and 7 cm. Find the area of the circle. (Take pi=3.14 ) एक वृत्त 24 cm और 7 cm भुजा वाले आयत के परिगत है। वृत्त का क्षेत्रफल ज्ञात कीजिए।( pi=3.14 )
02:48View SolutionA chord of length 24 cm is at a distance of 5 cm from the centre of a circle. What is its area? एक वृत्त के केंद्र से 5 सेमी की दूरी पर 24 सेमी लंबाई का एक जीवा है। इसका क्षेत्रफल क्या है?
02:04View Solution

