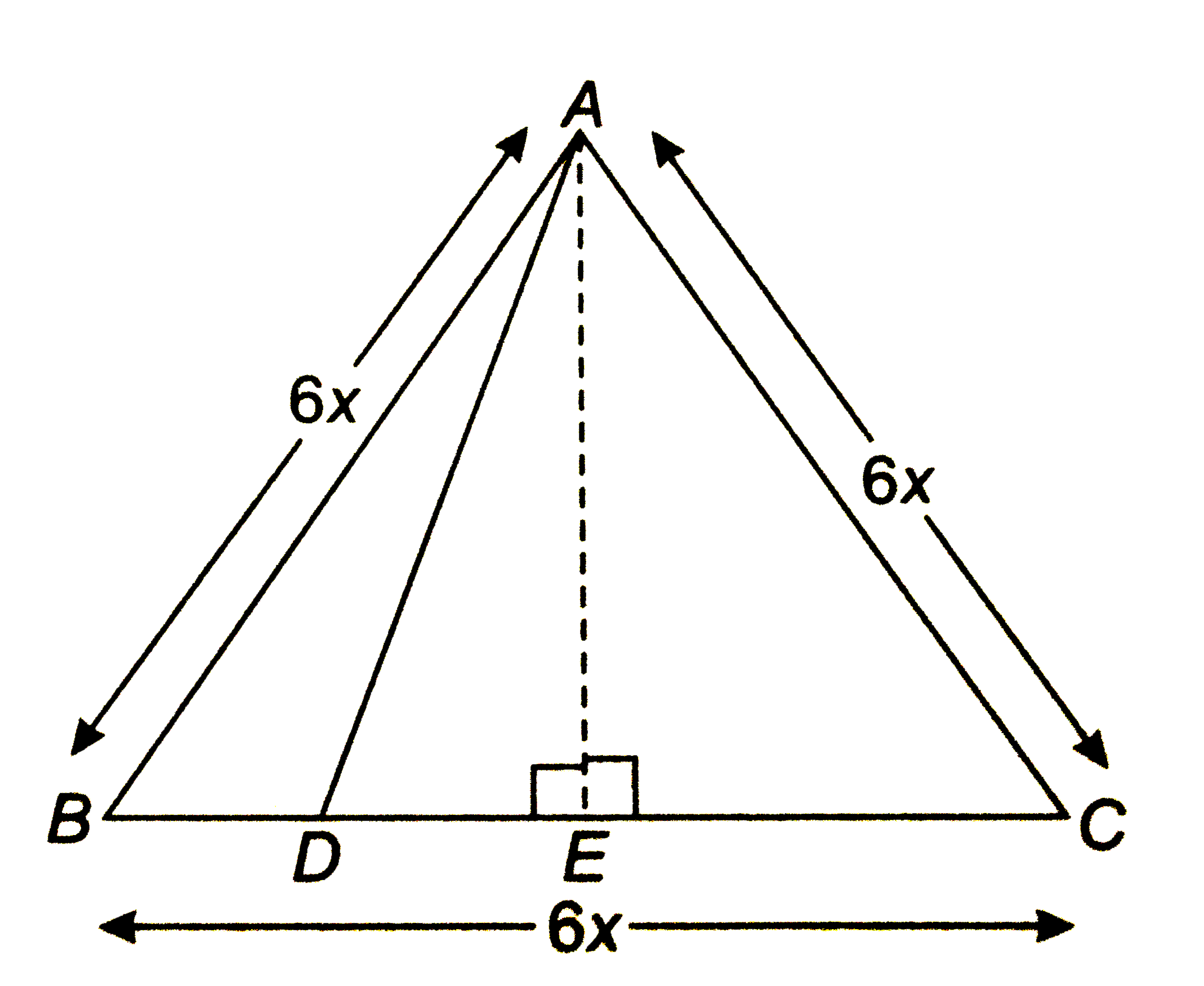
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BD=13BC है सिद्ध कीजिये कि 9AD2=7AB2 है
माना AB=BC=AC=6x
तथा BD=13BC=13×6x=2x
और BE=EC=BC2=3x
(∴ समबाहु त्रिभुज में लम्ब , आधार को समद्विभाजित करता है )
∴ DE=BE−BD=3x−2x=x
अब पाइथागोरस के प्रमेय से
(6x)2=AD2−x2+(3x)2
⇒AD2=36x2+x2−9x2=28x2
∴9AD2=9×28x2=9×7×4x2
=7×36x2=7(AB)2
⇒9AD2=7AB2 यही सिद्ध करना था
Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.6 (ऐच्छिक))
Explore 10 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविध प्रश्नावली (अति लघु उत्तरीय प्रश्न)
Explore 9 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
Explore 9 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग Book:NOOTAN HINDIChapter:त्रिकोणमिति के कुछ अनुप्रयोग Exercise:विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
Explore 6 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
Explore 7 Videos
Similar Questions
आकृति में PS कोण QPR का समद्विभाजक है सिद्ध कीजिये कि QSSR=PQPR है
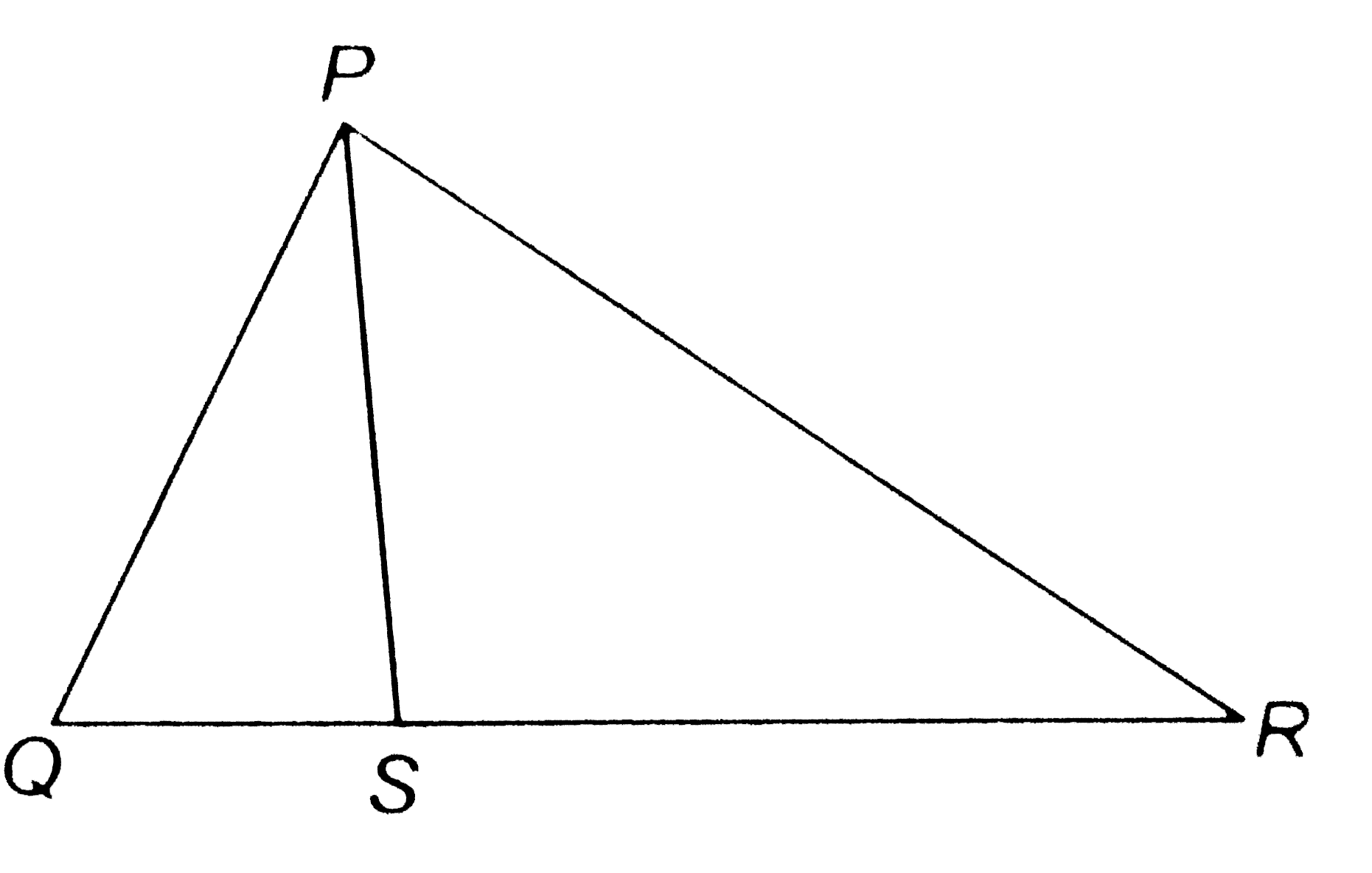
View SolutionΔABC की भुजाओ AC और BC पर क्रमशः दो बिंदु M और N है बताइये कि MN||BC है या नहीं यदि CM=4.2 सेमी, MA=2.8 सेमी, NB=3.6 सेमी, AN=5.7 सेमी
View Solutionमान लीजिये ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिये
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionIn an equilateral Triangle ABC,D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
View Solutionएक समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार है कि BD=13BC है सिद्ध कीजिए कि 9AD2=7AB2
View Solution

