किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिन्दु D इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है ( चित्र देखिये ) सिद्ध कीजिये कि 2AB2=2AC2+BC2 है
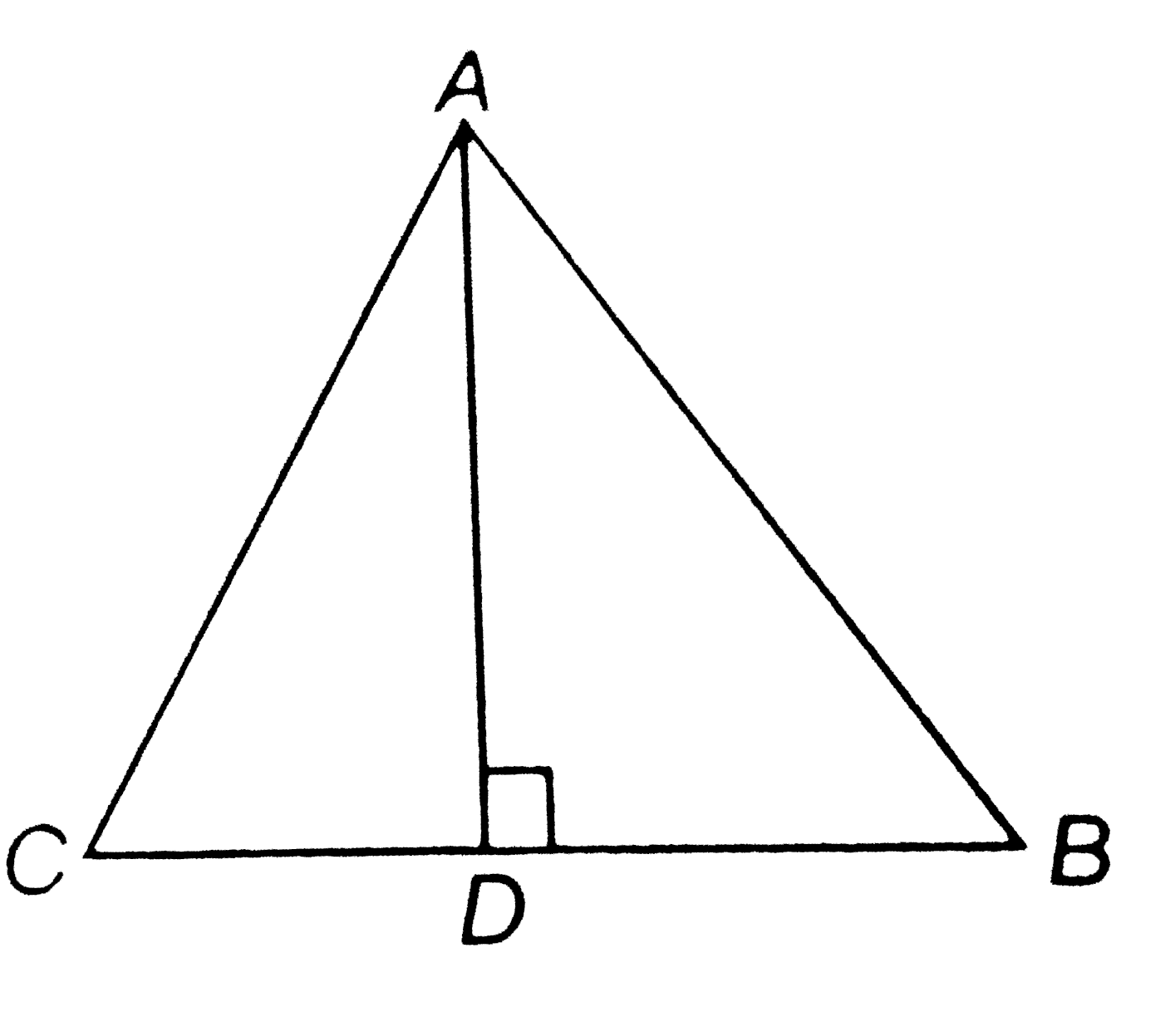
दिया है : ΔABC में AD⊥BC और DB=3CD
सिद्ध करना है 2AB2=2AC2+BC2
उपपत्ति : ∴DB=3CD⇒DBCD=31
माना DB=3x ⇒ CD=x
∴DBBC=3x4x=34⇒DB=34BC ...(1)
और DCBC=x4x=14⇒DC=14BC ...(2)
अब पाइथागोरस प्रमेय से
AB2=AD2+BD2=(AC2−DC2)+BD2 (पाइथागोरस प्रमेय से)
=AC2−116BC2+916BC2
=AC2+816BC2=AC2+12BC2
⇒2AB2=2AC2+BC2 यही सिद्ध करना था
Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.6 (ऐच्छिक))
10 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविध प्रश्नावली (अति लघु उत्तरीय प्रश्न)
9 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
9 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
6 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
Similar Questions
आकृति में PS कोण QPR का समद्विभाजक है सिद्ध कीजिये कि QSSR=PQPR है
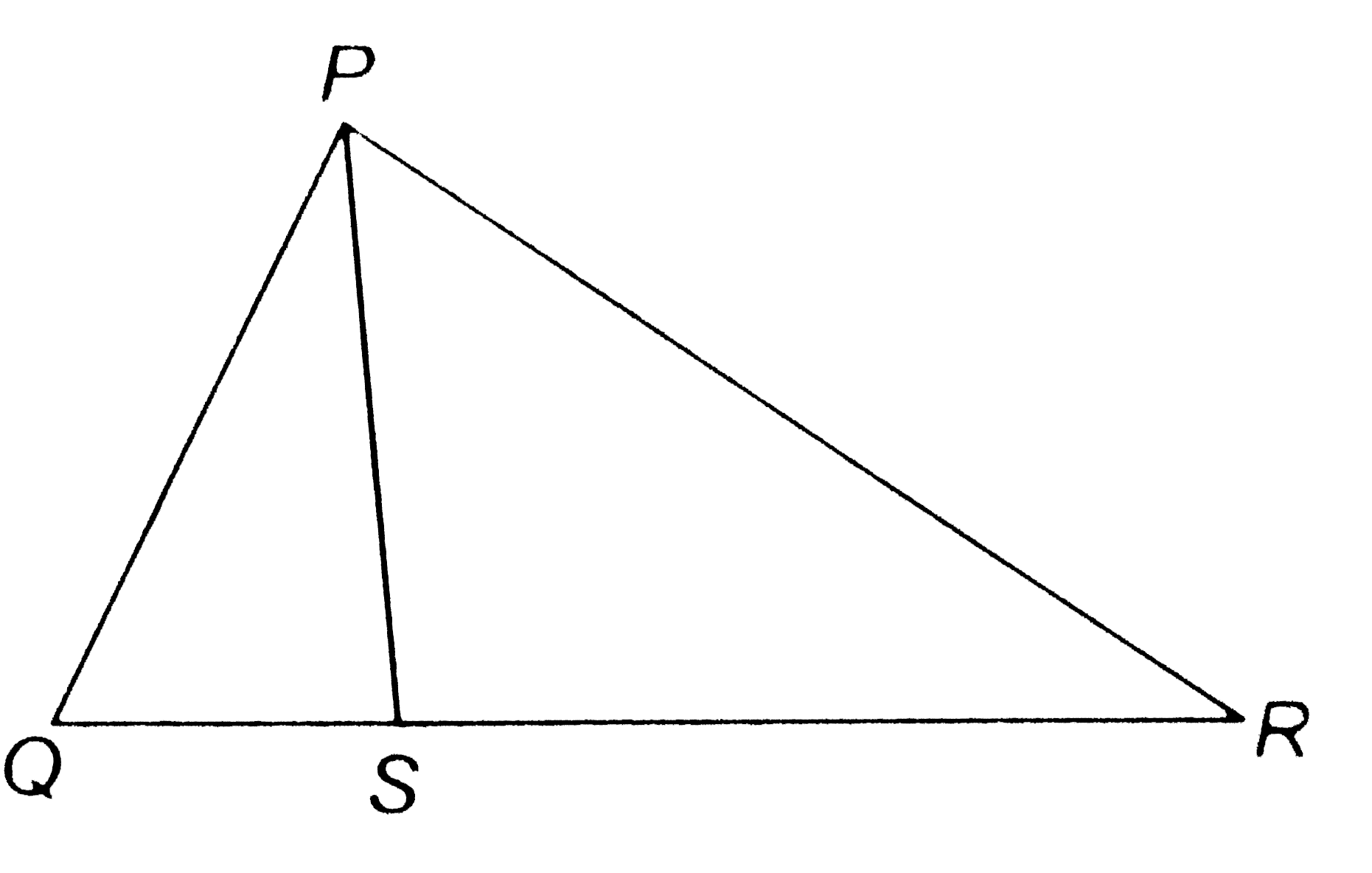
View SolutionΔABC की भुजाओ AC और BC पर क्रमशः दो बिंदु M और N है बताइये कि MN||BC है या नहीं यदि CM=4.2 सेमी, MA=2.8 सेमी, NB=3.6 सेमी, AN=5.7 सेमी
View Solutionमान लीजिये ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिये
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionThe perpendicular AD on the base BC of a ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View SolutionIn Delta ABC seg AD perp seg BC,DB=3CD Prove that 2AB^(2)=2AC^(2)+BC^(2)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, the of a ΔABC, interesects BC at D such DB=3CD. Prove that 2AB2=2AC2+BC2
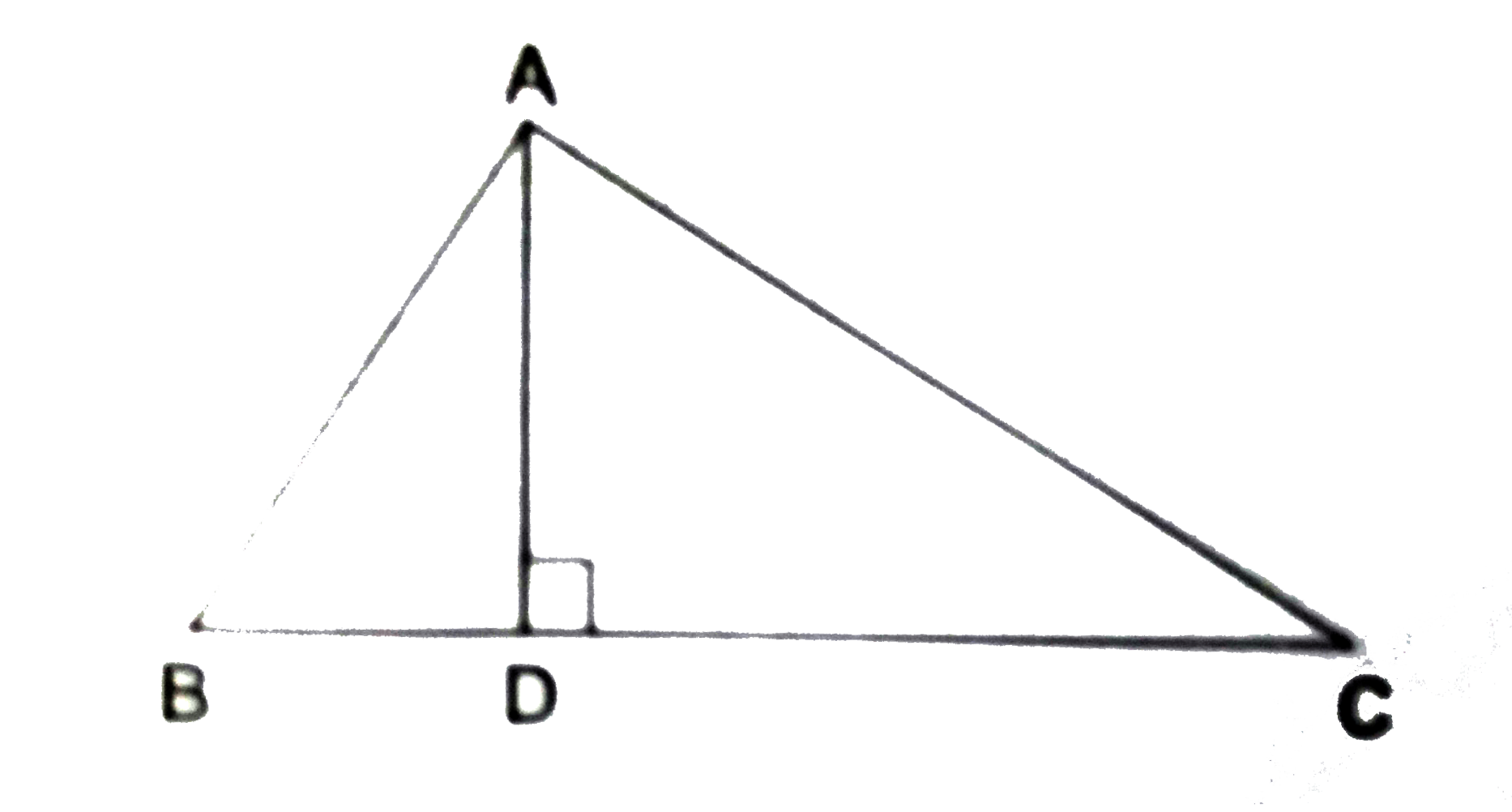
View SolutionΔABC के आधार BC पर डाला गया लंब AD भुजा BC को D पर प्रतिच्छेद करता है ।
यदि DB=3CD सिद्ध कीजिए कि 2AB2=2AC2+BC2.
View Solution
