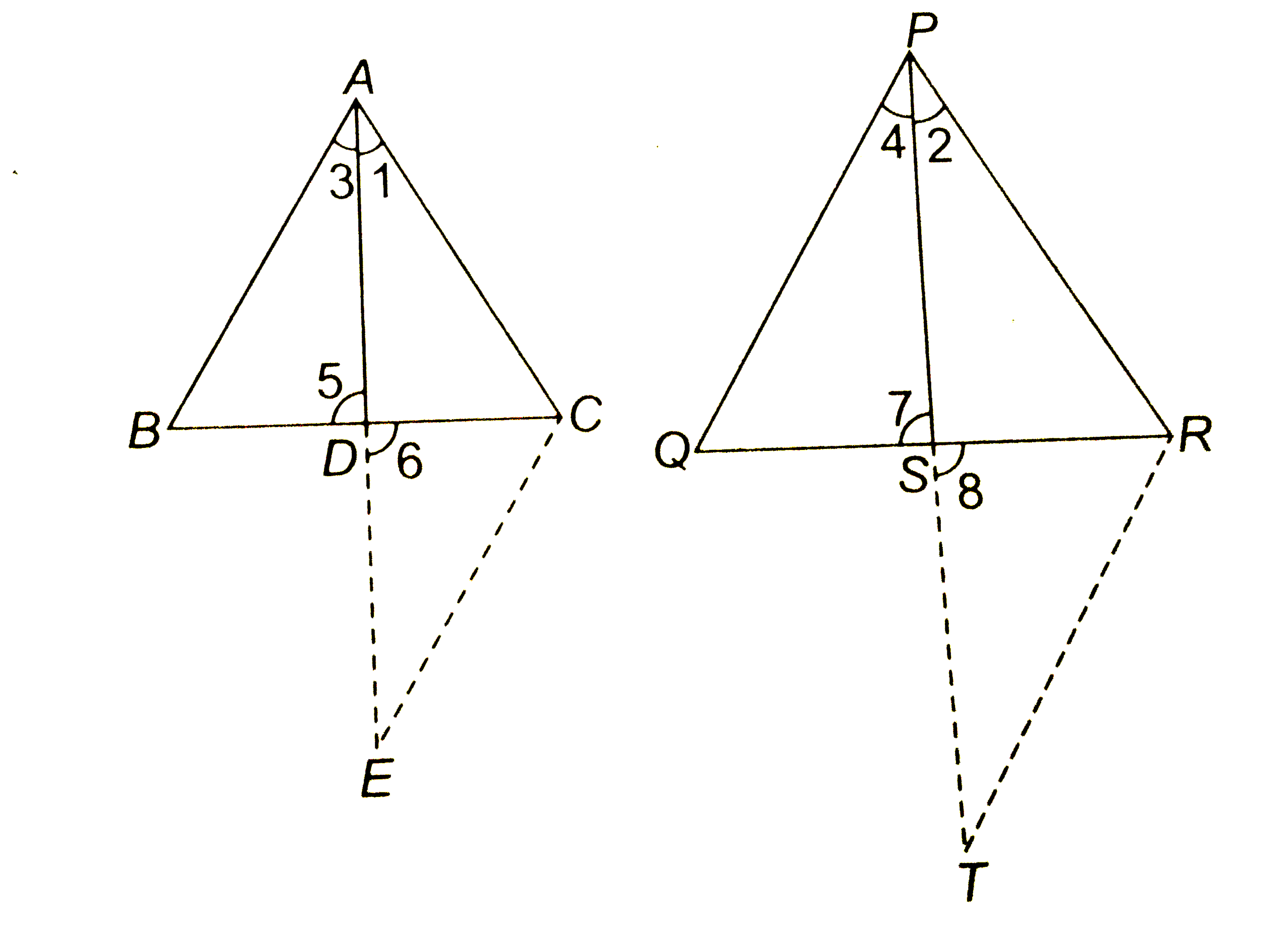
एक त्रिभुज ABC की भुजाये AB और AC तथा मध्यिका AD एक अन्य त्रिभुजों PQ और PR तथा मध्यिका PM के क्रमशः समानुपाती है दर्शाइए कि ΔABC~ΔPQR है
दिया है : ΔABC और ΔPQR जिसमे AD और PS मध्यिकाये इस प्रकार है कि
ABPQ=ACPR=ADPS
दर्शाना है : ΔABC~ΔPQR
रचना : AD को E तक इस प्रकार बढ़ाया कि AD = DE है EC को मिलाया PS को T तक इस प्रकार बढ़ाया कि PS = ST है TR को मिलाया
उपपत्ति : ΔABD और ΔECD
∴ BD=DC(∴D,BC का मध्य बिंदु है )∠5=∠6( शीर्षभिमुख कोण )AD=DE( रचना से )
∴ ΔABD≅ΔECD (S.A.S. सर्वांगसमता)
∴ AB=EC (सर्वांगसमता त्रिभुज के सर्वांगसम भाग बराबर होते है) ...(1)
इसी प्रकार सिद्ध कर सकते है कि
ΔPQS≅ΔTRS ∴ PQ=TR ...(2)
अब, ∴ABPQ=ACPR=ADPS (दिया है)
⇒ ECTR=ACPR=2AD2PS [समीकरण (1) और (2) से]
⇒ ECTR=ACPR=AEPT
∴ ΔAEC~ΔPTR (S.S.S. समरूपता)
∴ ∠1=∠2 (समरूप त्रिभुजों के संगत कोण बराबर होते है) ...(3)
इसी प्रकार सिद्ध कर सकते है कि
∠3=∠4 ...(4)
समीकरण (3) और (4) को जोड़ने पर
∠1+∠3=∠2+∠4 ⇒ ∠A=∠P
अब ΔABC और ΔPQR में
ABPQ=ACPR (दिया है)
और ∠A=∠P (अभी सिद्ध किया है)
∴ ΔABC~ΔPQR (S.A.S. समरूपता) यही दर्शाना था
Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
Explore 9 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.5)
Explore 17 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)
Explore 10 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग Book:NOOTAN HINDIChapter:त्रिकोणमिति के कुछ अनुप्रयोग Exercise:विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
Explore 6 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
Explore 7 Videos
Similar Questions
मान लीजिये ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिये
View Solutionकुछ त्रिभुजों कि भुजाये नीचे दी गयी है निर्धारित कीजिये कि इनमे से कोण-कोण से त्रिभुज समकोण त्रिभुज है इस स्थिति में कारण कि लम्बाई भी लिखिए
(i) 7cm,24cm,25cm
(ii) 3cm,8cm,6cm
(iii) 50cm,80cm,100cm
(iv) 13cm,12cm,5cm
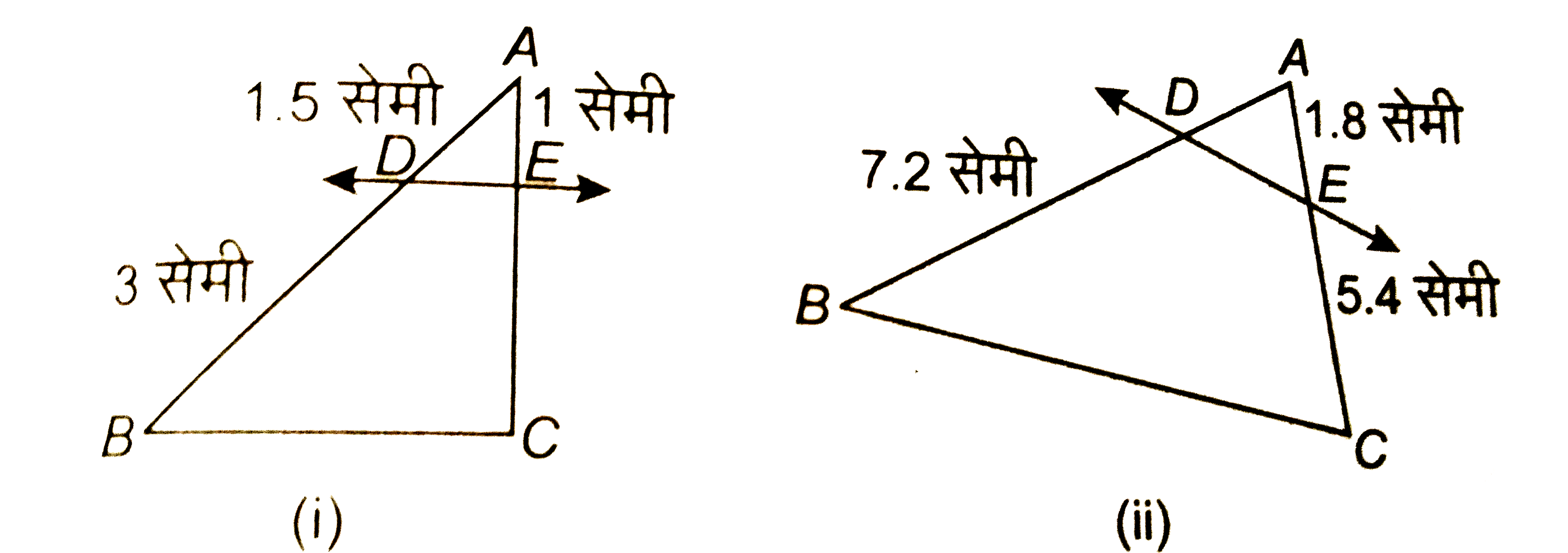
View Solutionआकृति (i) और (ii) में , DE || BC है (i) में EC और (ii) में AD ज्ञात कीजिये
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View Solutionयदि ΔABC और ΔPQR में ABPR=BCPR=CAPQ तो
View Solutionदर्शाइए कि सदिश 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆk और (3ˆi−4ˆj−5ˆk) एक समकोण त्रिभुज के शीर्षों कि रच्ना करते है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionIn triangle ABC , P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR: RQ =1: 2. If PR = 2cm, then BC =? triangle ABC में, P और Q क्रमशः भुजाओं AB तथा AC के मध्य बिंदु हैं। R, PQ पर एक बिंदु इस प्रकार है कि PR: RQ =1: 2 यदि PR=2 सेमी, तो BC=
View SolutionIn triangle ABC E and D are points on sides AB and AC,respectively, such that angle ABC= angle ADE , if AE = 6cm, AD = 4 cm and EB = 4 cm, then the length of DC is: triangle ABC में, E और D क्रमशः AB और AC पर एक बिंदु हैं, जैसे कि angle ABC= angle ADE ,यदि AE = 6cm, AD = 4 cm और EB = 4 cm है, तो DC की लंबाई है:
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionThe sides AB and AC of a triangle ABC are extended to P and Q respectively. If the bisectors of angle PBC and angle QCB intersect at O, and angle A=92^@ , then angle BOC is equal to: एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि angle PBC तथा angle QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा angle A=92^@ है, तो angle BOC किसके बराबर है ?
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution

