आकृति में AB = AC वाले , एक समद्विबाहु त्रिभुज ABC कि बढ़ाई गयी भुजा CB पर स्थित E बिंदु है यदि AD⊥BC और EF⊥AC है तो सिद्ध कीजिये कि ΔABD~ΔECF है
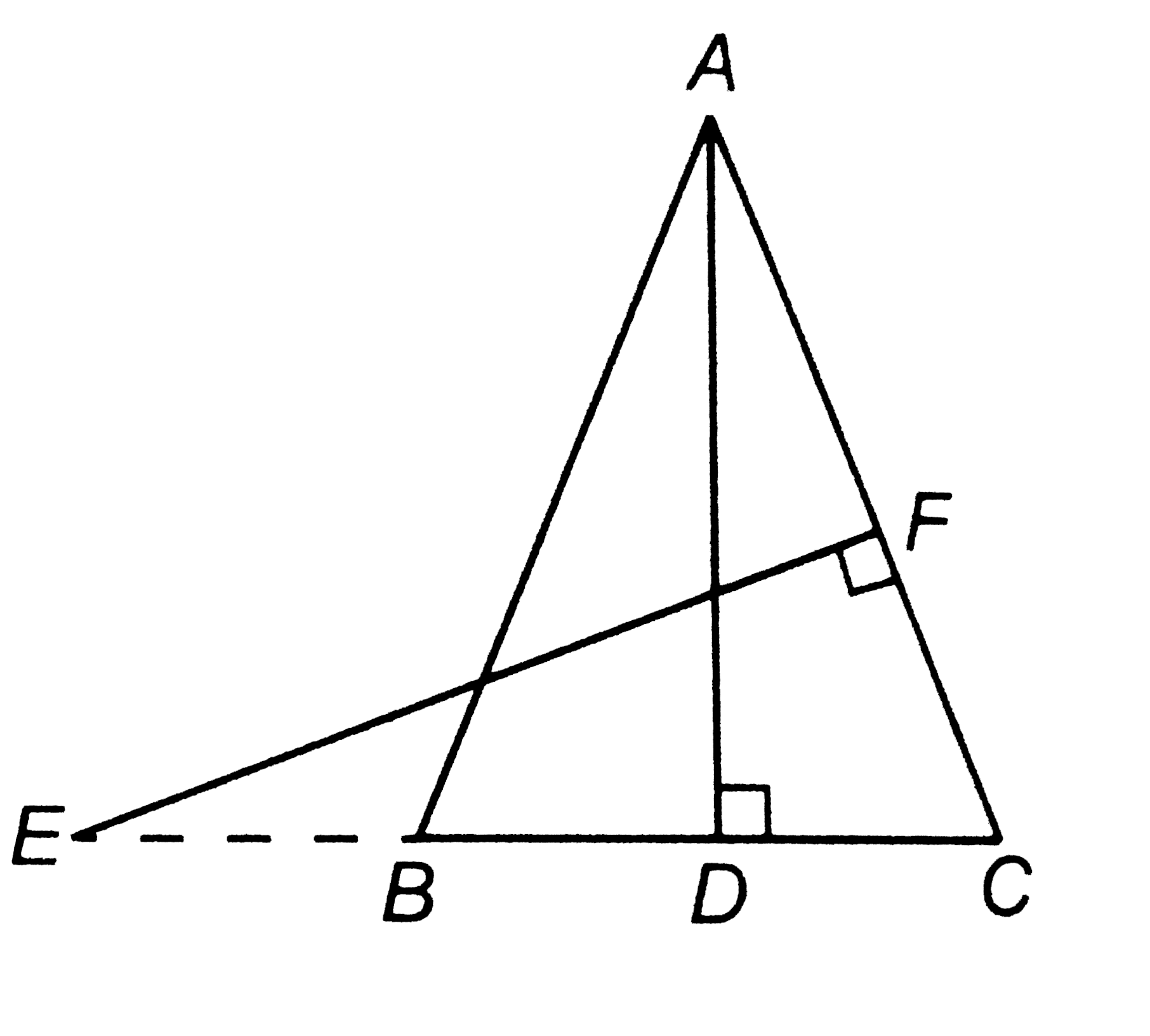
ΔABC समद्विबाहु है जिसमे , AB=AC
⇒ ∠ACB=∠ABC (सामान भुजाओ के सम्मुख कोण)
⇒ ∠ECF=∠ABD
तथा ∠EFC=∠ADB (प्रत्येक 90∘)
∴ ΔECF~ΔABD (A.A समरूपता से) यही सिद्ध करना था
Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
Explore 9 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.5)
Explore 17 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)
Explore 10 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग Book:NOOTAN HINDIChapter:त्रिकोणमिति के कुछ अनुप्रयोग Exercise:विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
Explore 6 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
Explore 7 Videos
Similar Questions
मान लीजिये ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिये
View Solutionकुछ त्रिभुजों कि भुजाये नीचे दी गयी है निर्धारित कीजिये कि इनमे से कोण-कोण से त्रिभुज समकोण त्रिभुज है इस स्थिति में कारण कि लम्बाई भी लिखिए
(i) 7cm,24cm,25cm
(ii) 3cm,8cm,6cm
(iii) 50cm,80cm,100cm
(iv) 13cm,12cm,5cm
View Solutionआकृति (i) और (ii) में , DE || BC है (i) में EC और (ii) में AD ज्ञात कीजिये
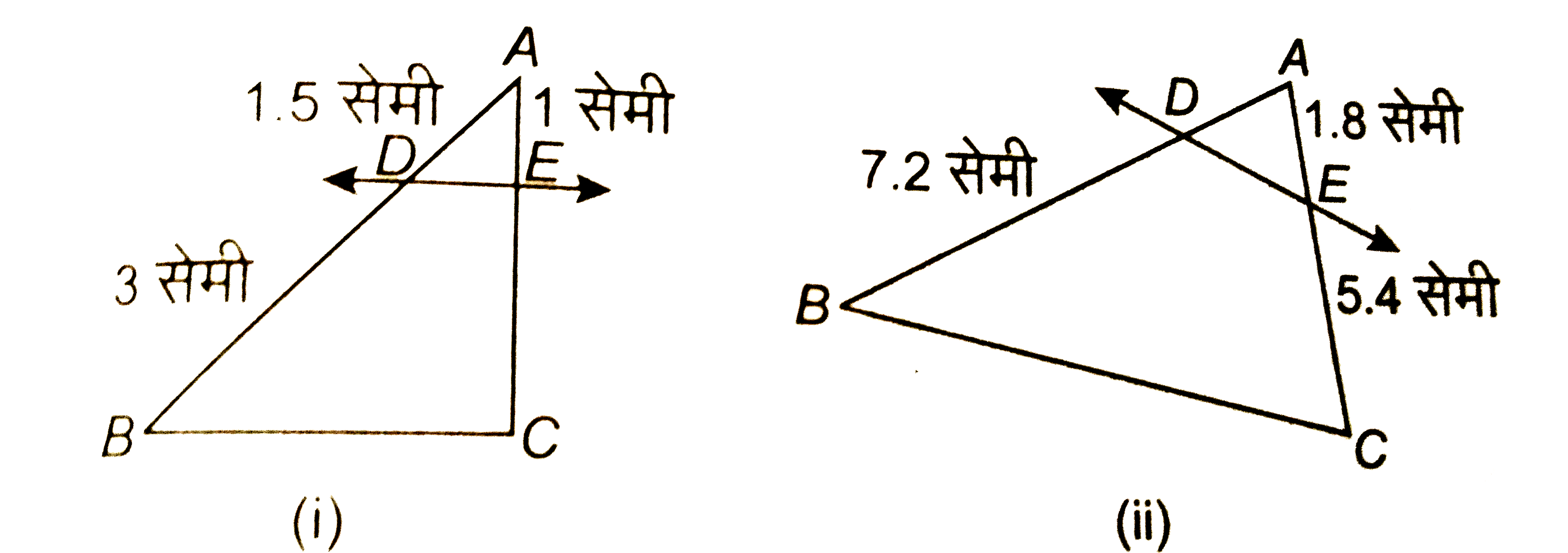
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionदी गयी आकृति में , AB = AC वाले एक समद्धिबाहु त्रिभुज ABC कि बढ़ाई गयी भुजा CB पर स्थित E एक बिन्दु है । यदि AD⊥BC और EF⊥AC है , तो सिद्ध कीजिए कि ΔABD~ΔECF है ।
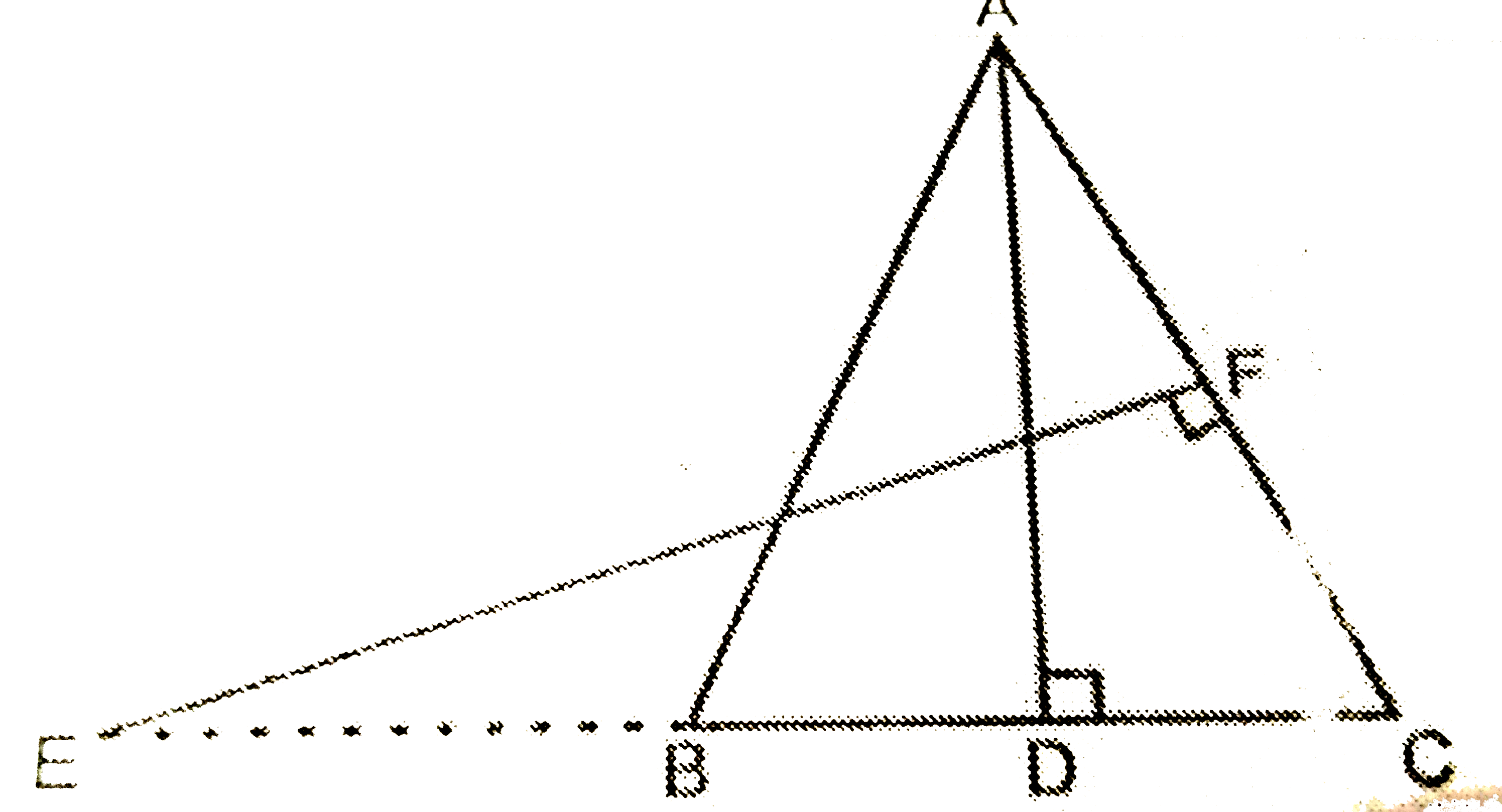
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solution

