एक गोलाकार चालक पर आवेश इस प्रकार वितरित है कि गोले के केंद्र से दूरी r पर आवेश के आयतन घनत्व p का मान निम्न है ,
p=p0(1−ra), जबकि 0<r<a तथा p=0 जबकि r>a, यहाँ P0, एक नियतांक है।
कुल वितरित आवेश की गणना कीजिए।
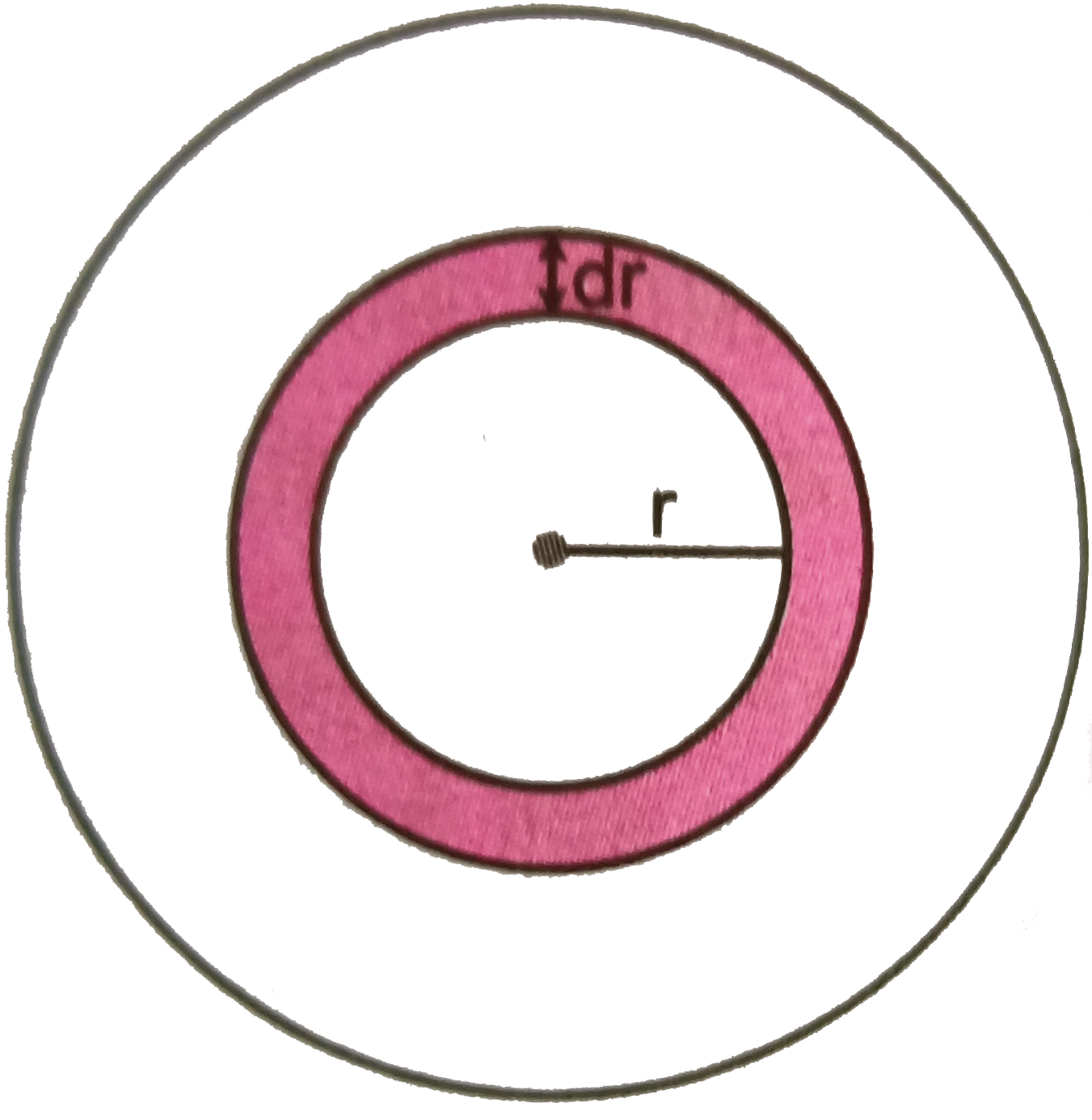
कुल वितरित आवेश की गणना करने के लिए माना गोलाकार चालक के अन्दर चित्र 1.35 की भाँति समकेन्द्रिक गोलीय खोल है जिसकी त्रिज्या r तथा मोटाई dr है।
गोलीय खोल का आयतन = 4πr2dr
गोलीय खोल में उपस्थित आवेश = p×4πr2dr=p0(1−ra)×4πr2dr
सम्पूर्ण गोले में वितरित कुल आवेश उपर्युक्त समीकरण को r= 0 से r= a तक समाकलित करके ज्ञात किया जा सकता है, अर्थात्
Q=∫a0p0(1−ra)×4πr2dr=4πp0∫a0(r2−r3a)dr
या Q=4πp0[r33−r44a]a0=3πp0[a33−a44a]=πp0a33
Topper's Solved these Questions
- विद्युत् आवेश तथा क्षेत्र BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - तथ्यात्मक प्रश्न
13 Videos
- विद्युत् आवेश तथा क्षेत्र BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - अभ्यास ( प्रत्येक प्रश्न में दिए गए विकल्पों में से सही विकल्प चुनिए )
15 Videos
- विद्युत-चुंबकीय तरंगे BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत-चुंबकीय तरंगे EXERCISE - वस्तुनिष्ठ प्रश्न
42 Videos
- विद्युत् विभव तथा धारिता BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् विभव तथा धारिता EXERCISE - इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए
166 Videos
Similar Questions
सू्खे बालों पर कंघी करने पर कंघी में कागज के छोटे-छोटे टुकड़ों को अपनी ओर आकर्षित करने का गुण आ जाता है, क्यों ? यदि बाल गीले हों तब क्या होगा ?
View Solutionधनावेशित काँच की छड़ को अनावेशित चालक से स्पर्श कराया जाता है। छड़ की आवेश :
View Solutionविद्युत-चुंबकीय तरंगों का आविष्कार किया था :
View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
VP−VQ तथा VB−VA

View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionआवेश || आवेश के प्रकार || आवेश के गुण
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionआवेश व उसके प्रकार#!# आवेश के गुणधर्म और उस पर आधारित प्रशन #!# आवेश को उत्पन करने की विधिया
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
View Solutionकूलॉम के नियम पर आधारित प्रश्न |आवेश घनत्व के प्रकार |प्रश्न |विद्धुत क्षेत्र |OMR|Summary
View Solutionआवेश#!#आवेश के प्रकार #!#आवेश के गुण
View Solution
