A 0.10 kg block oscillates back and forth along a horizontal surface. Its displacement from the origin is given by: x=(10cm)cos[(10rads)t+π/2rad] what is the maximum accelration experiends by the block
10m/s2
10πm/s2
10π2m/s2
10π3m/s2
The correct Answer is:A
a=10×10−2 m and ω=10 rad/sec
Amax=ω2a=10×10−2×102=10m/sec2
Topper's Solved these Questions
Similar Questions
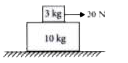
A 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
View SolutionIf the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?
View Solution
Knowledge Check
A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
A10ms−2B100ms−2C200ms−2D0.1ms−2A 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=10ms−2)
 A134,0.6B144,3C134,3D143,0.6
A134,0.6B144,3C134,3D143,0.6A block is attached to a horizontal spring and oscillates back and forth on f frictionless horizontal surface at a frequency of 3.00Hz. The amplitude of the motion is 5.08×10−2m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits?
A5.08×10−2m,4.24HzB3.59×10−2m,4.24HzC2.54×10−2m,3.00HzD3.59×10−2m,6.00Hz
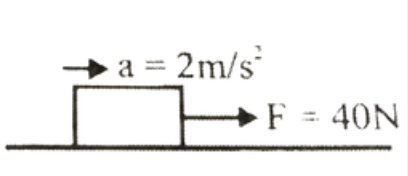
A block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View SolutionIf the phase angle for a block -spring system in SHM is π/8 rad and the block's position is given by x=xmcos(ωt+ϕ), what is the ratio of the kinetic energy to the potential energy at time t= 0?
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View SolutionThe displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+1.5π)
The motion of the particle is
View Solution
