Light with wavelength 535nm falls normally on a diffraction grating. Find its period if the diffraction angle 35∘ corresponds to one of the Fraunhofer maxima and the highest order of spectrum is equal to five.
The diffraction fromula is
dsinθ0=n0λ
where θ0=35∘ is the angle of diffraction corresponding to order n0 (which is not yet known).
Thus d=n0λsinθ0=n0×0.9327μm
on using λ=0.535μm
For the nth order we get
sinθ=nn0sinθ0=nn0(0.573576)
If n0−1, then n>n0 is at least 2 and sinθ>1 so n=1 is the highest order of diffraction.
If n0=2 then n=3,4, but sinθ>1 for n=4 thus the highest order of diffraction is 3.
If n0=3,
then n=4,5,6.
For n=6,sinθ=2×0.57>1, so not allowed while for
n=5,sinθ=53×0.573576<1
is allowed. Thus in this case the highest order of diffraction is five as given. Hence
n0=3
and d=3×0.9327=2.7981≈2.8μm.
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Find the wavelength of monochromatic light falling normally on a diffraction grating with period d=2.2μm if the angle between the directions to the Fraunhofer maxima of the first and the second order is equal to Δθ=15∘.
View SolutionLight with wavelength 530nm falls on a transparent diffraction grating with period 1.50μm. Find the angle, relative to the grating normal. At which the Fraunhofer maximum of highest order is observed provided the light falls on the grating
(a) at right angles,
(b) at the angle 60∘ to the normal.
View Solution
Knowledge Check
A beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
AλdBdλC2λdD2dλLight is incident normally on a diffraction grating through which the first order diffraction is seen at 32∘. The second order diffraction will be seen at
A(a) 48∘B(b) 64∘C(c) 80∘D(d) There is no second order diffraction in this case.
Light with wavelength λ falls on a diffracting grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle θ.
View SolutionLight with wavelength λ=589.0nm falls normally on a diffraction grating with period d=2.5μm, comprising N=10000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionSodium light of wavelength 5890 Å is incident normally on a diffraction grating of 5000 rulings per cm. Find the angle of diffraction for the second order.
View SolutionLight composed of two spectral lines with wavelength 600.00 and 600.050nm falls normally on a diffraction grating 10.0mm wide. At a centain diffraction angle θ these lines are close to being resolved (according to Rayleigh's criterion). Find θ.
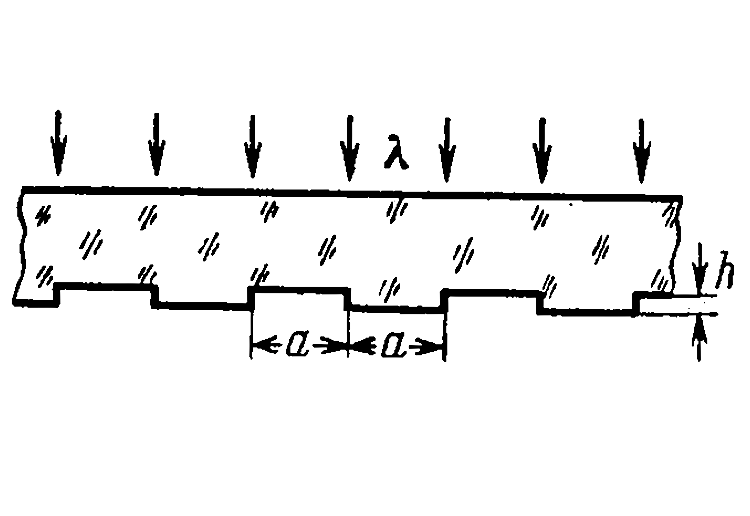
View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionLight of wavelength 500 nm falls normally on a slit of width 1μm producing Fraunhofer diffraction pattern on a screen. Calculate the angular position of the first minimum and the angular width of the central maximum.
View Solution
