Light with wavelength λ=0.60μm falls normally on a diffraction grating inscribed on a plane surfcae of a plano-curvex cylinderical glass lens with curvature radius R=20cm. The period of the grating is equal to d=6.0μm. Find the distance between the principle maxima of first order located symmetrically in the focal plane of that lens.
For the lens
1f=(n−1)(1R−1∞) or f=Rn−1
For the grating
dsinθ1=λ or sinθ1=λd
cosecθ1=dλ,cotθ1=√(dλ)2−1
tanθ1=1√(dλ)2−1
Hence the distance between the two symmetrically placed first order maxima
=2ftanθ1=2R(n−1)√(dλ)2−1
On putting R=20,n=1.5,d=6.0μm
λ=0.60μm we get 8.04cm.
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Polarization Of Light
Explore 43 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Dispersion And Absorption Of Light
Explore 24 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Interference Of Light
Explore 33 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
Light with wavelength λ=589.0nm falls normally on a diffraction grating with period d=2.5μm, comprising N=10000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionFind the positions of the perinciple planes, the focal and model points of a thin biconvex symmetric glass lens with curvature radius of its surfaces equal to R=7.50cm. There is air on one side of the lens and water on the other.
View SolutionA beam of X-rays with wavelength λ=40± falls normally on aplne rectangular array of scattering centres and produces a system of diffraction maxima (Fig.) on a plane screen removed from the array by a distance l=10cm. Find the array periods a and b along the x and y axes if the distance between symmetrically located maxima of second order are equal to Δx=60mm (along the x axis) and Δy=40mm (along the yaxis).

View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
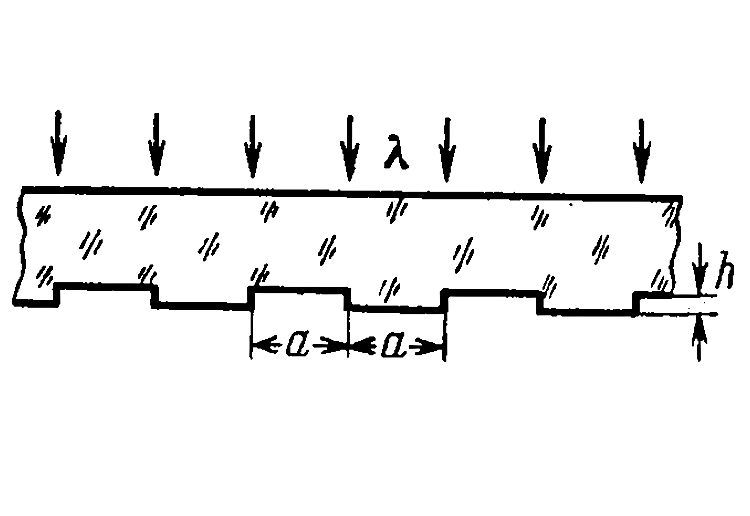
View SolutionFind the wavelength of monochromatic light falling normally on a diffraction grating with period d=2.2μm if the angle between the directions to the Fraunhofer maxima of the first and the second order is equal to Δθ=15∘.
View SolutionA plane light wave with wavelength λ=0.50μm falls normally on the face of a glass wedge with an angle Θ=30∘. On the opposite face of the wedge a transparent diffraction grating with period, d=2.00μm is inscibed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light froms with the directions to the principle Fraunhofer maxima of the zero and the first order. waht is the highest order of the spectrum? At what angle to the direction of incident light of the observed?
View SolutionCalculate the positions of the principle planes and focal points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to R1=10.0cm and of the concave surface to R2=5.0cm and the lens thickness is d=3.0cm.
View SolutionA slit of width 0.025 mis placed in front of a lens of focal length 50 cm. The slit is illuminated with light of wavelength 5900 Å. Calculate the distance between the centre and first dark band of diffraction pattern obtained on a screen placed at the focal plane of the lens.
View SolutionA plane light wave with wavelength λ=0.57μm falls normally on a suface on a surface of a glass (n=1.60) disc which shuts one and a half Fresnel zones for the observation point P. What must the minimum thickness of that disc be for the intensity of light at the point P to be the highest ? Take into account the interference of light on its passing through the disc.
View SolutionFind the radius of curvature of convex surface of a plano convex lens, whose focal length is 0.3mandμ=1.5.
View Solution

