Two coherent plane light waves propagating with a divergence angle psi

Light of wavelength $λ$ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is ––
A $\frac{d^{2}}{λ}$
B $\frac{2 d}{λ}$
C $\frac{2 d^{2}}{λ}$
D $\frac{d^{2}}{2 λ}$
Two coherent sources $S_{1}$ and $S_{2}$ are kept on the edges of a step as shown in the figure. An infinitely long screen is placed on the right side of sources and lies at along $y - z$ plane. Calculate total no. of maximas observed on the screen. $P S_{1} = 8 λ$ and $P S_{2} = 6 λ$ . Where $λ$ is wavelength of light used. (There is no reflection from steps)

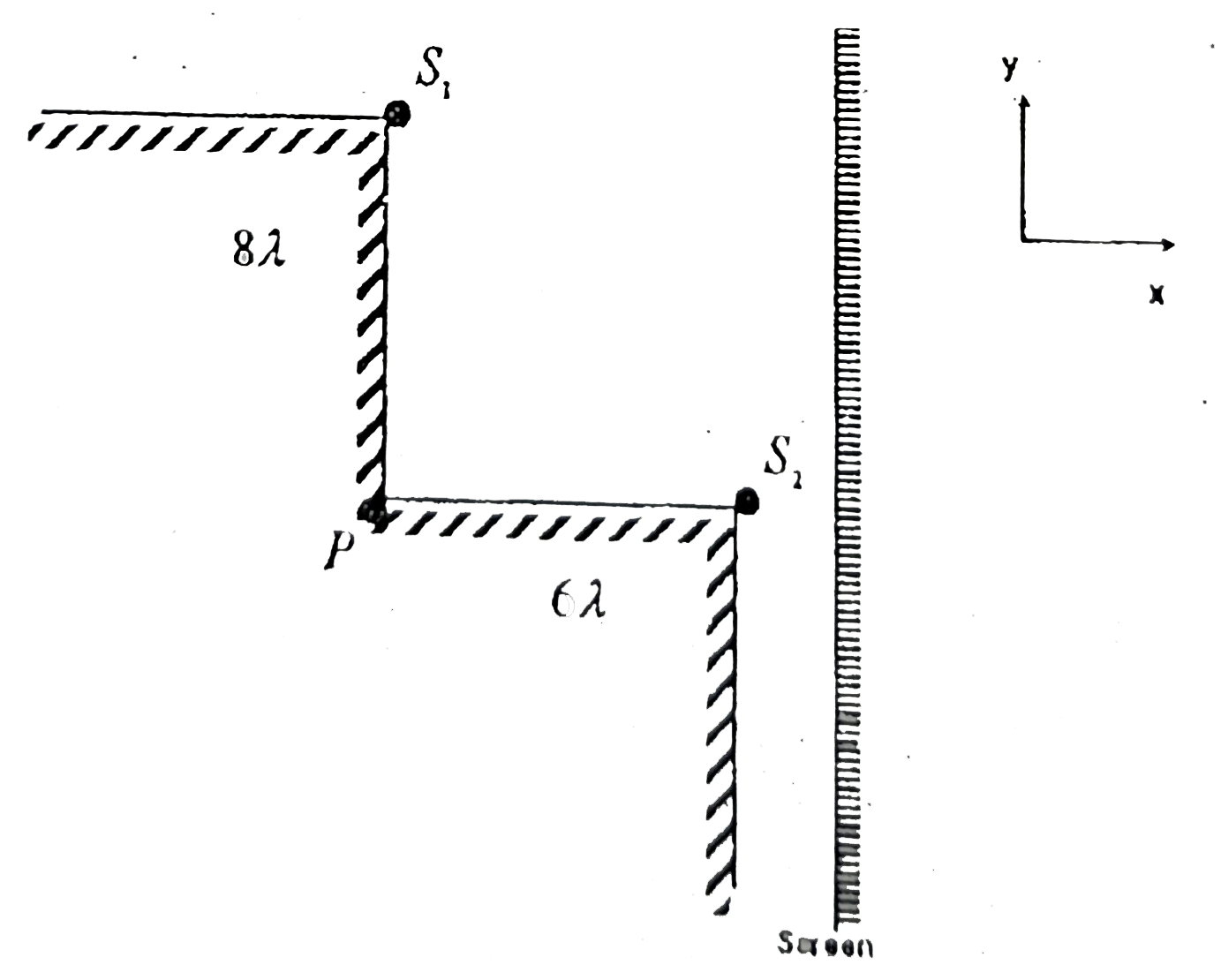A $18$
B $16$
C $14$
D $12$

Two coherent plane light waves propagating with a divergence angle $ψ < < 1$ fall almost normally on a screen. The amplitudes neighbouring maxima on the screen is equal to $Δ x = λ / ψ$ , where $λ$ is the wavelength.