Write the law of reflection of a light beam from a mirror in vector from, using the directing unit vectors e and e' of the incident and reflected beams and the unit vector n of the outside normal to the mirror surrfcae.
To express the law of reflection in vector form using the unit vectors of the incident beam e, the reflected beam e′, and the unit normal vector n to the mirror surface, we can follow these steps:
1. Define the Incident and Reflected Vectors:
- Let e be the unit vector in the direction of the incident beam.
- Let e′ be the unit vector in the direction of the reflected beam.
- Let n be the unit normal vector to the surface of the mirror.
2. Decompose the Incident Vector:
- The incident vector e can be decomposed into two components: one parallel to the mirror surface and one perpendicular to it.
- The perpendicular component can be expressed as:
e⊥=(e⋅n)n
- The parallel component is then:
e∥=e−e⊥=e−(e⋅n)n
3. Reflection of the Perpendicular Component:
- Upon reflection, the perpendicular component changes direction. Thus, the reflected perpendicular component e′⊥ becomes:
e′⊥=−e⊥=−(e⋅n)n
4. Reflection of the Parallel Component:
- The parallel component remains unchanged in direction:
e′∥=e∥
5. Combine the Reflected Components:
- The reflected vector e′ can now be expressed as the sum of the reflected parallel and perpendicular components:
e′=e′∥+e′⊥=e∥−(e⋅n)n
- Substituting e∥:
e′=(e−(e⋅n)n)−(e⋅n)n
6. Final Expression:
- Simplifying the expression gives:
e′=e−2(e⋅n)n
Conclusion:
The law of reflection in vector form is given by:
e′=e−2(e⋅n)n
- Let e be the unit vector in the direction of the incident beam.
- Let e′ be the unit vector in the direction of the reflected beam.
- Let n be the unit normal vector to the surface of the mirror.
- The incident vector e can be decomposed into two components: one parallel to the mirror surface and one perpendicular to it.
- The perpendicular component can be expressed as:
e⊥=(e⋅n)n
- The parallel component is then:
e∥=e−e⊥=e−(e⋅n)n
- Upon reflection, the perpendicular component changes direction. Thus, the reflected perpendicular component e′⊥ becomes:
e′⊥=−e⊥=−(e⋅n)n
- The parallel component remains unchanged in direction:
e′∥=e∥
- The reflected vector e′ can now be expressed as the sum of the reflected parallel and perpendicular components:
e′=e′∥+e′⊥=e∥−(e⋅n)n
- Substituting e∥:
e′=(e−(e⋅n)n)−(e⋅n)n
- Simplifying the expression gives:
e′=e−2(e⋅n)n
The law of reflection in vector form is given by:
e′=e−2(e⋅n)n
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Interference Of Light
Explore 33 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Diffraction Of Light
Explore 60 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
Knowledge Check
If a,b, and c are the unit vectors along the incident ray, reflected ray and the outward normal to the reflector. Then
Ab=a=cBb=a+(a.c)cCb=2a−cDb=a−2(a.c)cWhich one of the following is the correct angle between the
incident and reflected rays when a ray of light incident
normally on a plane mirror?Aa 180∘Bb 90∘Cc 45∘Dd 0∘If a light ray is reflected from a mirror as shown in the figure, then
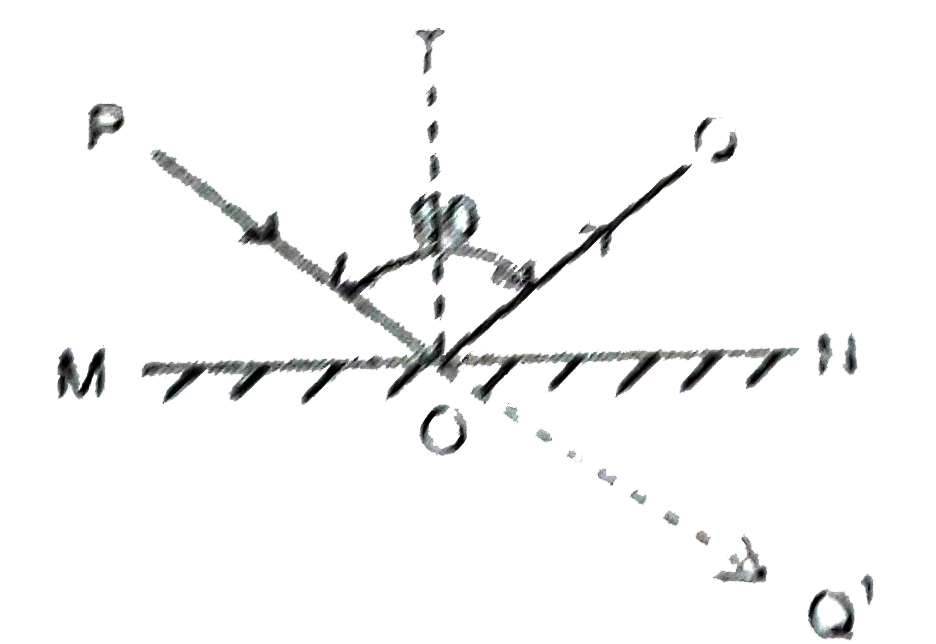 Athe glancing angle of light ray is 45∘Bthe reflected light ray is perpendicular to the incident light ray.Cthe incident ray is deviated through an angle of 90∘DAll of the above
Athe glancing angle of light ray is 45∘Bthe reflected light ray is perpendicular to the incident light ray.Cthe incident ray is deviated through an angle of 90∘DAll of the above
Find the vector equation of a plane at a distance of 5 units from the origin and has ˆi as the unit vector normal to it.
View SolutionFind the vector equation of a plane which is at a distance of 3 units from the origin and has ˆk as the unit vector normal to it.
View SolutionIf a light ray is reflected from a mirror as shown in the figure, then

View SolutionDuring the reflectio of ligth from plane mirror, the incident ray, normal and reflected ray lie
View SolutionAssertion:− Unit vector is used to describe a direction in space.
Reason:− Unit vector has a unit through its magnitude is one.
View Solution

