A current flows along a round loop. Find the intergal along the axi so the loop within the range from to . Expain the result obtained.
On the axis, , along the axis.
Thus.
, on putting
The physicall interpreation of this result is that can be thought of as teh circulation of over a closed loop by imaging that the two ends of the axis are connected by a line at inifinity (e.g, a semicircle of infinitate radius ).
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A current I flows along a round loop. Find the integral ∫→B.→dr along the axis of the loop within the range from (−∞) to (+∞). Explain the result obtained.
View SolutionA small current-carrying coil having a megantic moment pm is located at the axis of a round loop of radius R with current I flowing thorough it. Find the magnitude of the vector force applied to the coil if its distance from the centre of the loop is equal to x and the vector pm coincides in direction with the axis of the loop.
View Solution
Knowledge Check
A current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
Aμ0IB4μ0ICμ0I2Dμ0I4A current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
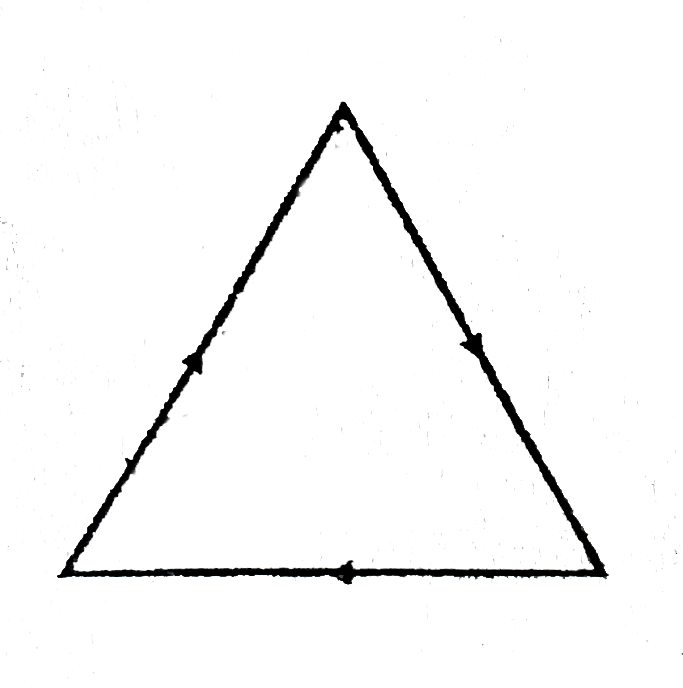 A3μ012πaB9μ0I2πaC(3√3μ0I)/(2πa)D3μ0I4πa
A3μ012πaB9μ0I2πaC(3√3μ0I)/(2πa)D3μ0I4πaA current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
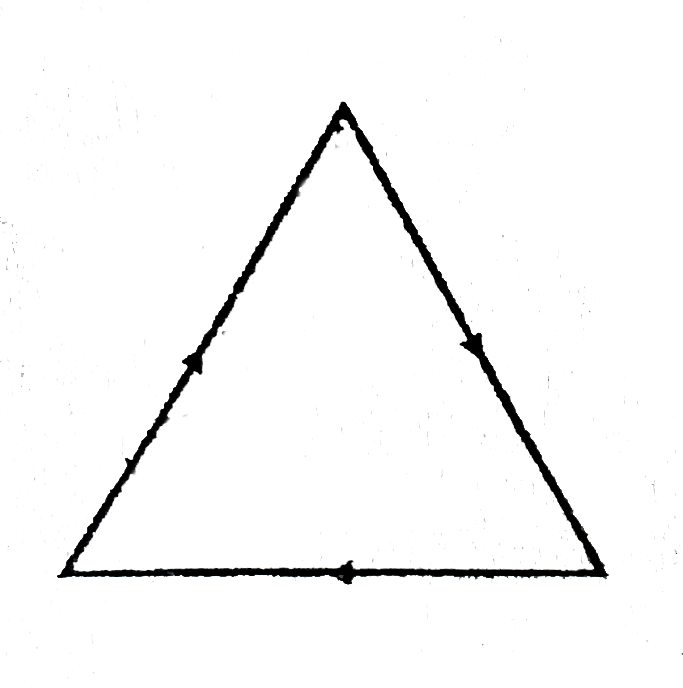 A3μ0I2πaB9μ0I2πaC3√3μ0I2πaD3μ0I4πa
A3μ0I2πaB9μ0I2πaC3√3μ0I2πaD3μ0I4πa
There is one circular current carrying loop. A charged particle is projected with a certain speed along the axis of the coil. How will the coil exert magnetic force on the charged particle?
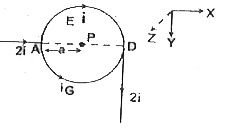
View SolutionIn the shown figure a current 2i is flowing in a straight conductor and entering along the diameter of the circular loop of similar conductor through the point A. The current is leaving the loop along another similar semi-infinite conductor parallel to the plane of the loop through the point D. what is the magnetic field at the centre of the loop P ?
View SolutionThe electric current flowing in a wire in the direction from B to A decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.

View SolutionA square loop of side 6cm carries a current of 30A. Calculate the magnitude of magnetic field B at a point P lying on the axis of the loop and a distance√7 cm from centre of the loop.
View SolutionThe current flows from A to B as shown in the figure The direction of the induced current in the loop is :

View Solution
