A thin insulated wire forms a plane spiral of turns carrying a current . The inner and outer radii are equal to . Find the magnetic induction at the centre of the spiral

(a) From Biot-Savart's law, the magnetic induction due to a circular current carrying wire loop at its centre is given by,
The plane spiral is made up of concentric circular loops, having different radii, varying from to Therefore, the total magentic induction at the centre,
.....(1)
where is the contribution of one turn of radius and is the number of turns in the interval
Substibuiting is equaction (1) and intergrating the result over between and , we obtain,
(b) The magetic moment of a turn of radius is and of all turns,
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Current
Explore 72 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A thin insulated wire forms a plane spiral of N=100 tight turns carrying a current I=8mA.The radii of inside and outside turns (figure) are equal to a=50mm and b=100mm.
(a)The magnetic induction at the centre of the spiral is NμT.Then find value of N.
(b)The magnetic moment of the spiral with a given current is NmAm2.Then find value of N.

View SolutionFind the magnetic dipole moment of the spiral of total number of turnsN, carrying current i having inner and outer radii a and b respectively.

View Solution
Knowledge Check
A thin insulated wire forms a plane spiral of N = 100 tight turns carrying a current I = 8 mA. The radii of inside and outside turns are equal to a = 50 mm and b = 100 mm. Find the magnetic moment of the spiral with a given current
 A15Am2B10Am2C30Am2D5Am2
A15Am2B10Am2C30Am2D5Am2A coil of self inductance 20 mH, having 50 turns, carries a current of 300 mA. If the area of the coil is 2cm2, the magnetic induction at the centre of the coil is
A7.5×10−3TB7.5×10−2TC6×10−1TD0.5TWhat is the magnetic moment of a current carrying thin circular loop if the radius of the loop is equal to R and the magnetic induction at its centre is equal to B ?
A2πBR3μ0B4πBR3μ0CBR2μ0DπBR3μ0
Find the magnetic dipole moment of the spiral of total number of turnsN, carrying current i having inner and outer radii a and b respectively.

View SolutionWhen a long wire carrying a steady current is best into a circular coil of one turn, the magnetic induction at its centre is B. When the same wire carrying the same current is bent into a circular coil of one turn, the magnetic induction at its centre is B. when the same wire carrying the same current is bent to form a circular coil of a turns of a smaller radius, the magnetic induction at the centre will be
View SolutionA long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is
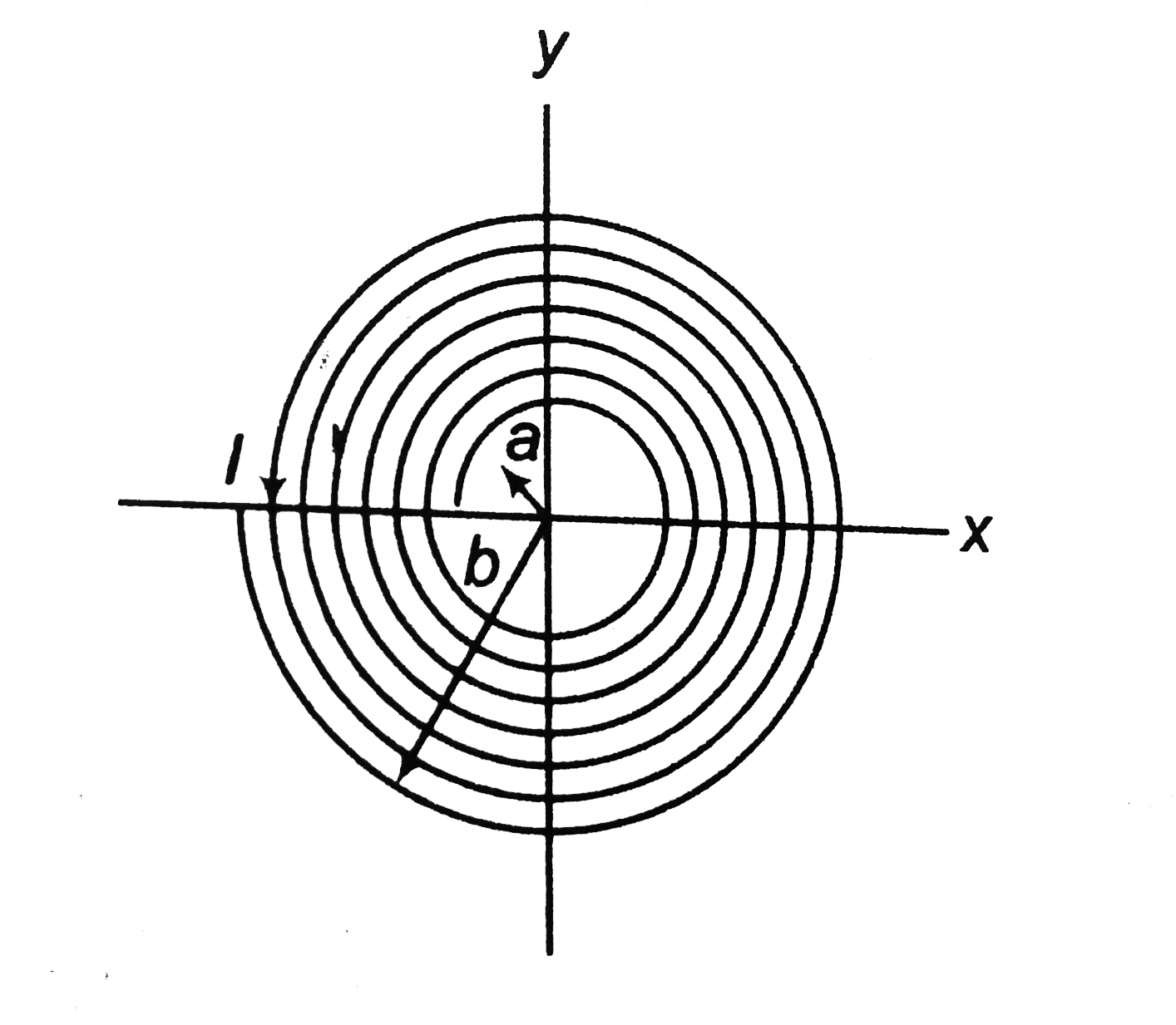
View SolutionA long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is

View SolutionA toroidal coil has 3000 turns. The inner and outer radii are 10 cm and 12 cm respectively. If current flowing is 5 A, then the magnetic field inside the toroid will be
View Solution

