From the Maxwell distribution function frind <<v2x>>, the mean value of the squared vx projection of the molecular velocity in a gas at a temperature T. The mass of each molecule is equal to m.
<v2x>=∫∞0v2xe−mv2x2ktdvx/∫∞0e−mv2x2ktdvx
=2kTm∫∞0xe−xdx2√x/∫∞0e−xdx2√x
=2kTmΓ(32)/Γ(12)=kTm.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:The Second Law Of Thermodynamics - Entropy
Explore 47 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Liquids Capillary Effects
Explore 25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:The First Law Of Thermodynamics - Heat Capacity
Explore 36 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Making use of the Maxwell distribution function, find <<1/v>>, the mean value of the reciprocal of the velocity of molecules in an ideal at a temperature T, it the mass of eacd molecule is equal to m. Compare the value obtained with the reciprocal of the mean velocity.
View SolutionUsing the Maxwell distribution function, calculate the mean velocity projection (vx) and the mean value of the modules of this projection <<|vx|>> if the mass of each molecule is equal to m and the gas temperature is T.
View Solution
Knowledge Check
The root mean square velocity of a gas molecule at any temperature T K of a gas molecule of molecular weight M is
A√8RT/MB√2RT/MC√3RT/MDzeroLet V denote the root mean square speed of the molecules in an ideal diatomic gas at absolute temperature T. The mass of a molecule is m. Neglecting vibrational energy terms, which is True?
Aa molecule can have a speed greater than √2vBv is proportional to √TCthe average rotational kinetic energy of a molecule is mv24Dthe average kinetic energy of a molecule is 5mv26Let ¯v,vrmsandvp respectively denote the mean speed. Root mean square speed, and most probable speed of the molecules in an ideal monatomic gas at absolute temperature T. The mass of a molecule is m. Then
Ano molecules can have a speed greater than √2vrmsBno molecule can have a speed less than vp/√2Cvp<¯v<vrmsDthe average kinetic energy of a molecules is 34mv2p.
For the following distribution function F (X) of a r.v. X
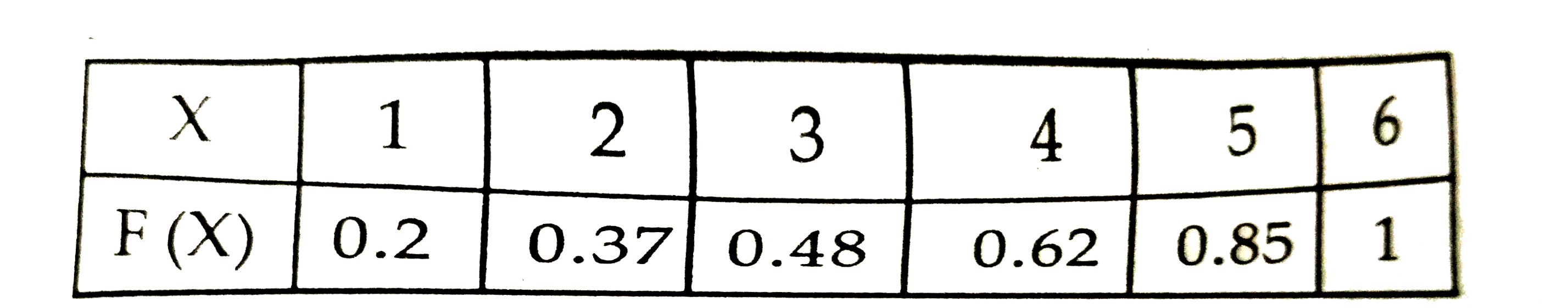
P(3<X≤5)=
View SolutionMaking use of the Maxwell distribution function, calculate the number v of gas molecules reaching a unit area of a wall per unit time, if the concentration of molecules is equal to n, the temperature to T, and the mass of each molecule is m.
View SolutionThe root mean square velocity of a gas molecule of mass m at a given temperature is proportional to
View SolutionLet →v,vrmsandvp respectively denote the mean speed, the root mean square speed and the most probable speed of the molecules in an ideal monatomic gas at absolute temperature T. The mass of a molecule is m. Then
View SolutionThe root mean square velocity of a gas molecule of mass m at a given temperature is proportional to
View Solution

