A cannon and a target are 5.10 k m apart and located at the same level. How soon will the shell launched with the initial velocity 240 m / s reach the target in the absence of air drag?

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is: 0.41 or 0.71 min later, depending on the initial angle.

Total time of motion
τ = 2 v 0 sin α g or sin α = τ g 2 v 0 = 9 ⋅ 8 τ 2 × 240 (1)
and horizontal range
R = v 0 cos α τ or cos α = R v 0 τ = 5100 240 τ = 85 4 τ (2)
From Eqs. (1) and (2)
( 9 ⋅ 8 ) 2 τ 2 ( 480 ) 2 + ( 85 ) 2 ( 4 τ 2 ) 2 = 1
On simplifying τ 4 - 2400 τ 2 + 1083750 = 0
Solving for τ 2 we get:
τ 2 = 2400 ± 1425000 2 = 2400 ± 1194 2
Thus τ = 42.39 s = 0.71 min and
τ = 24.55 s = 0.41 min depending on the angle α .

Updated on:21/07/2023
|
Class 12PHYSICSPHYSICAL FUNDAMENTALS OF MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A bullet of mass 10 g leaves a rifle at an initial velocit of 1000 m/s and strikes a target at the same level with a velocity of 100 m/s. The work done in joule to overcome the resistance of air will be

    A5000
    B3750
    C500
    D375

  • A cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-

    A4u2sin2θ5g
    Bu2sin2θ5g
    C3u2sin2θ5g
    D8u2sin2θ5g

  • Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
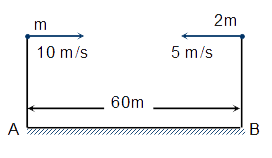    ocr_image

    A40 m
    B20 m
    C30 m
    Dzero