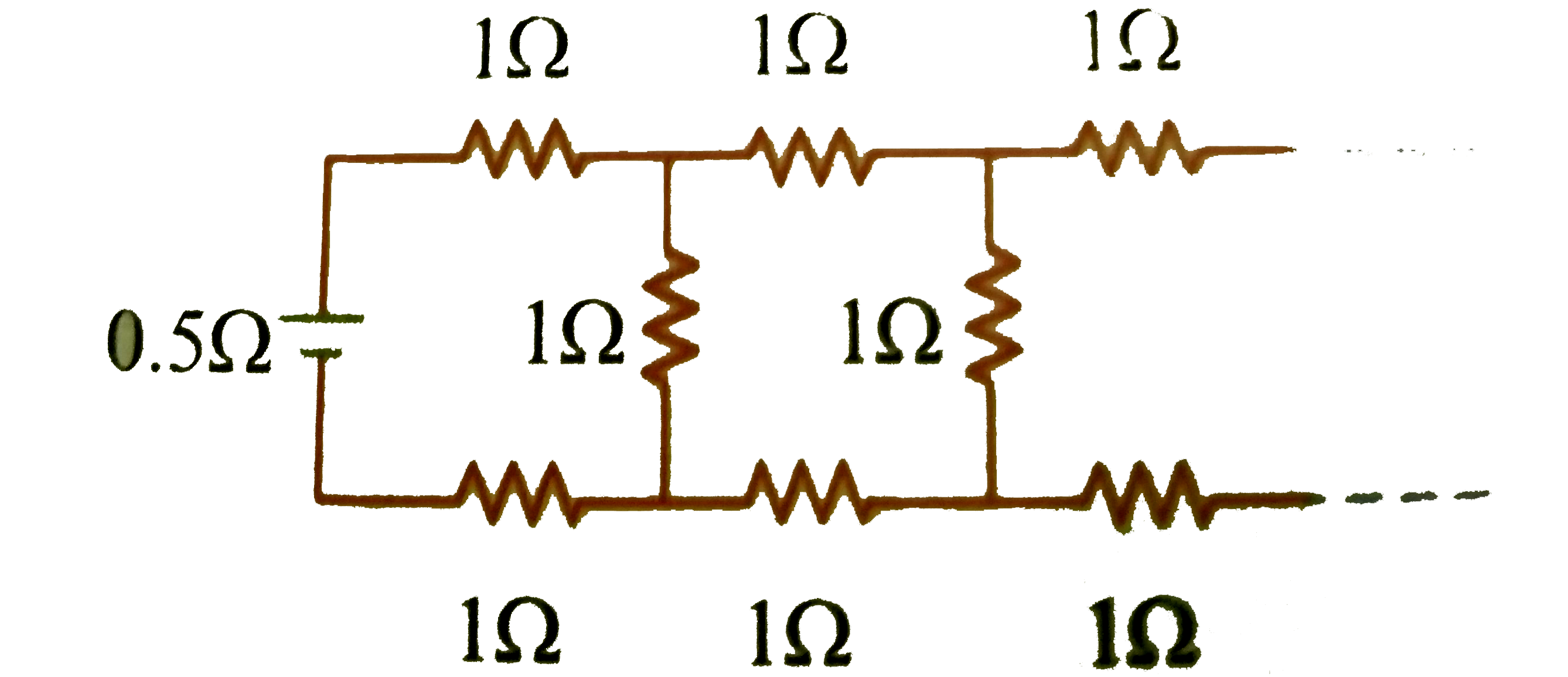
Determine the current drawn from a 12V supply with internal resistance 0.5Ω. By the infinite network shown in fig. Each resistor has 1Ω resistance.
Let x be the equivalent resistance of infinite net work. Since the net work is infinite, therefore, the addition of one more unit of three resistance each of value of 1Ω across the terminals will not alter the total resistance of net work, i.e., it should remain x.
Therefore, the network would appear as shown in Fig.2(NCT).4 and its total resistance should remain x. Here the parallel combination of x and 1Ωis in series with the two resistors of 1Ωeach. The resistance of paralle combination is
1Rp=1x+11=1+xxorRp=xx+1
∴ Total resistance of net work will be given by x=1+1+xx+1=2+xx+1orx(x+1)=2(x+1)+xorx2+x=2x+2+xorx2−2x−2=0orx=2±√4+82=2±√122=2±2√32=1±√3
The value of resistance can not be negative, therefore, the resistance of net work =1+√3=1+1.73Ω=2.73Ω
Total resistance of the circuit =2.73+0.5=3.23Ω.: Current drawn, l=123.23=3.72 amp
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Determine the current drawn from a 12V supply with internal resistance 0.5Ω by the infinite network shown in Fig. Each resistor has 1Ω resistance
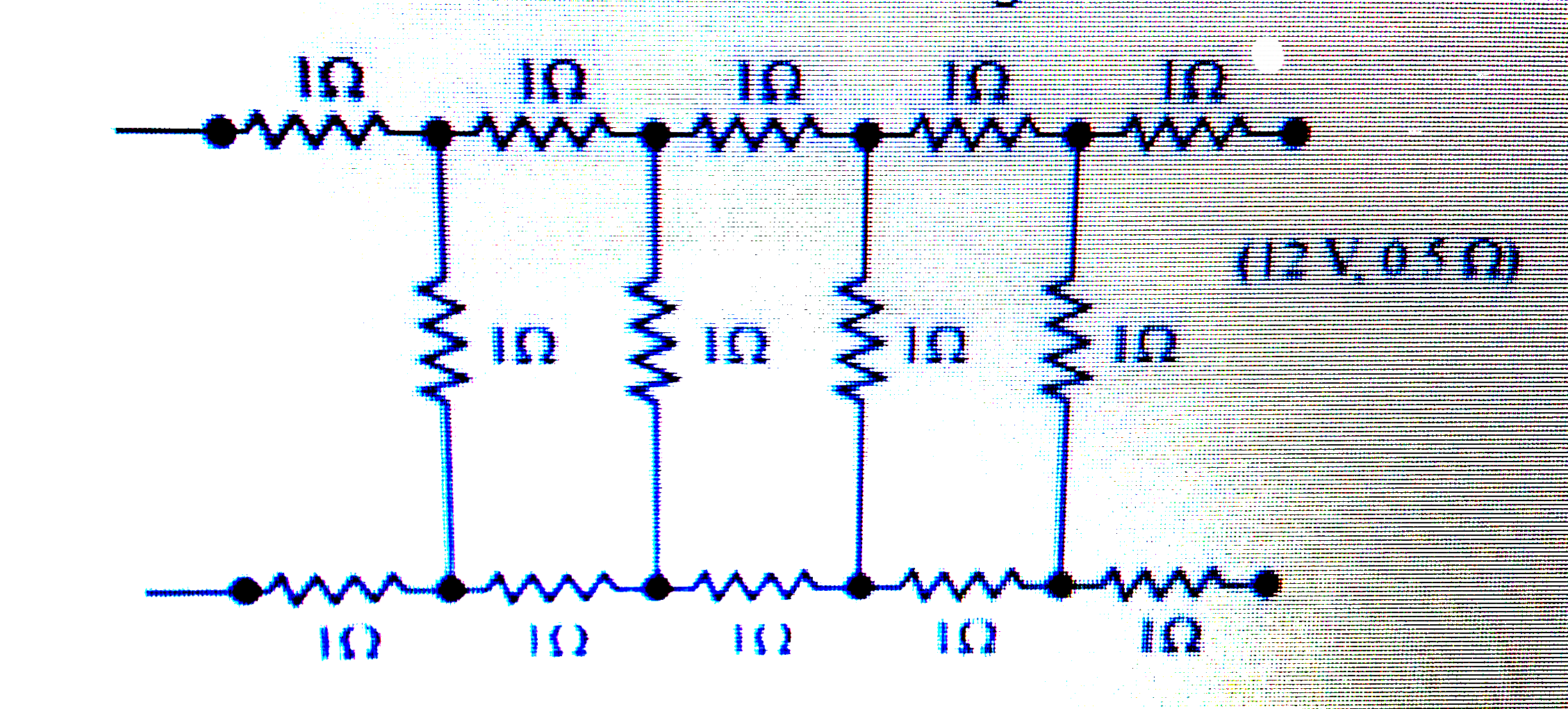
View SolutionDetermine the current drawn from a 12 V supply with internal resistance 0.5Ω by the infinite network shown in Fig. Each resistor has 1Ω resistance.

View Solution
Knowledge Check
A 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor isA0.27AP2→P1B0.03AP1→P2C0.03AP2→P1D0.27AP1→P27 V battery with internal resistance 2Ωand3V battery with internal resistance 1Ω are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
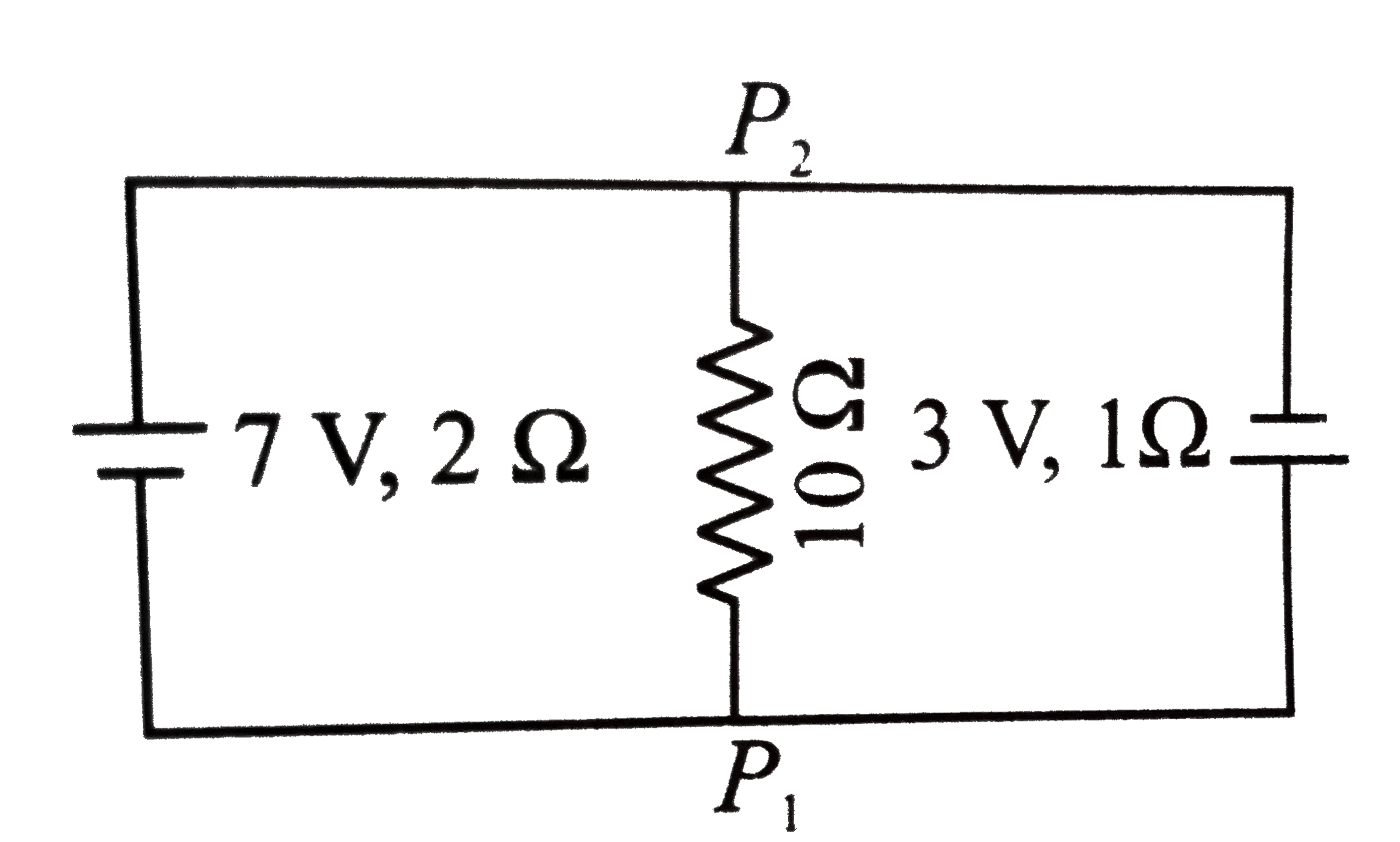 A0.27AB0.31AC0.031AD0.53
A0.27AB0.31AC0.031AD0.53Six equal resistances, each 1Ω, are joined to form a network as shown in fig. Then the resistance between any two corners is
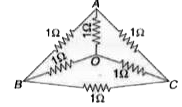 A0.5ΩB2ΩC1ΩD1.5Ω
A0.5ΩB2ΩC1ΩD1.5Ω
Find the current drawn from a cell of emf 1 V and internal resistance (2/3)Ω connected to the network shown in figure

View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
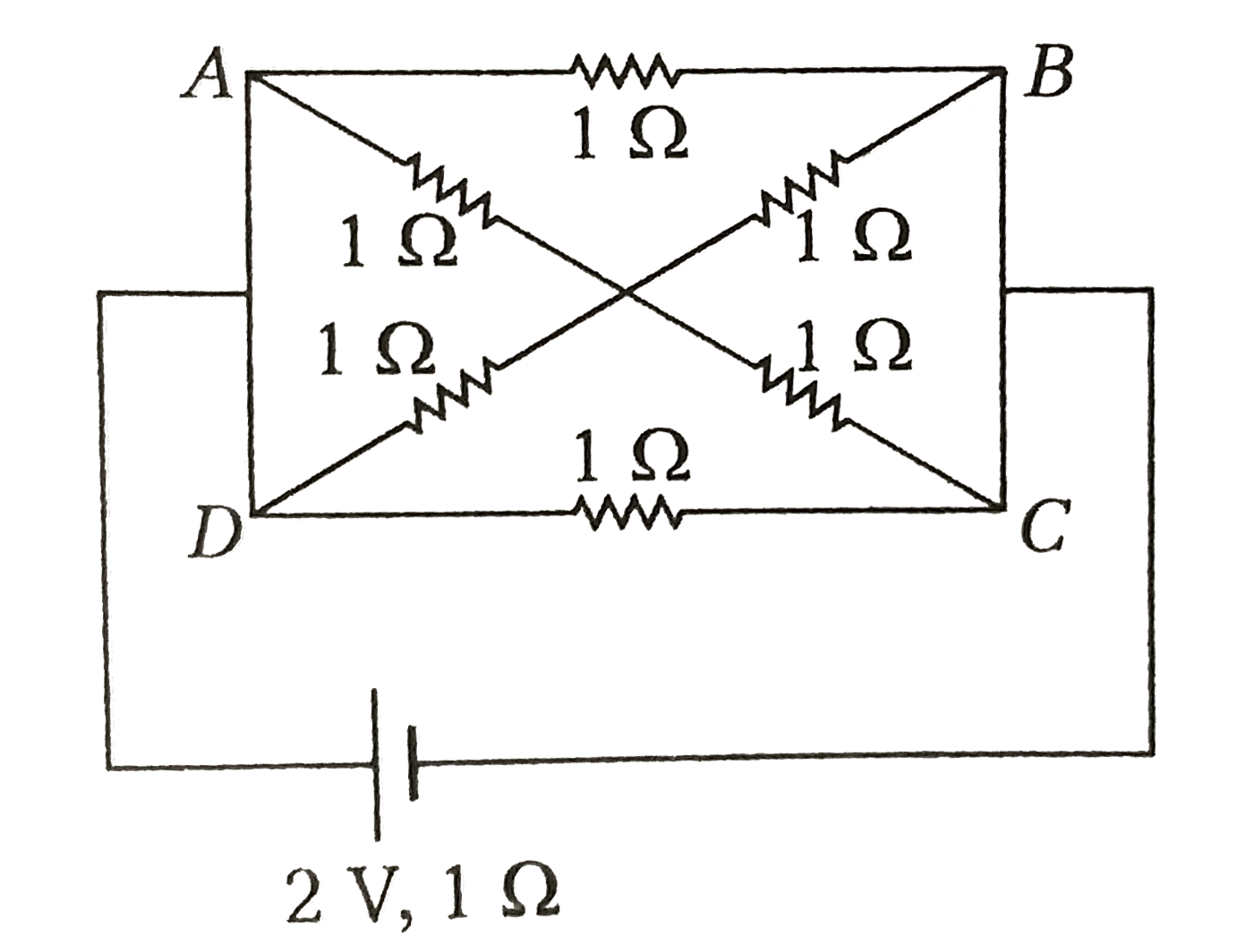
View SolutionCalculate the current drawn from the battery of emf 15V and internal resistance 0.5Ω in the circuit shown in Fig. 6.12. Also find the power dissipated in thd 6Ω resistor.
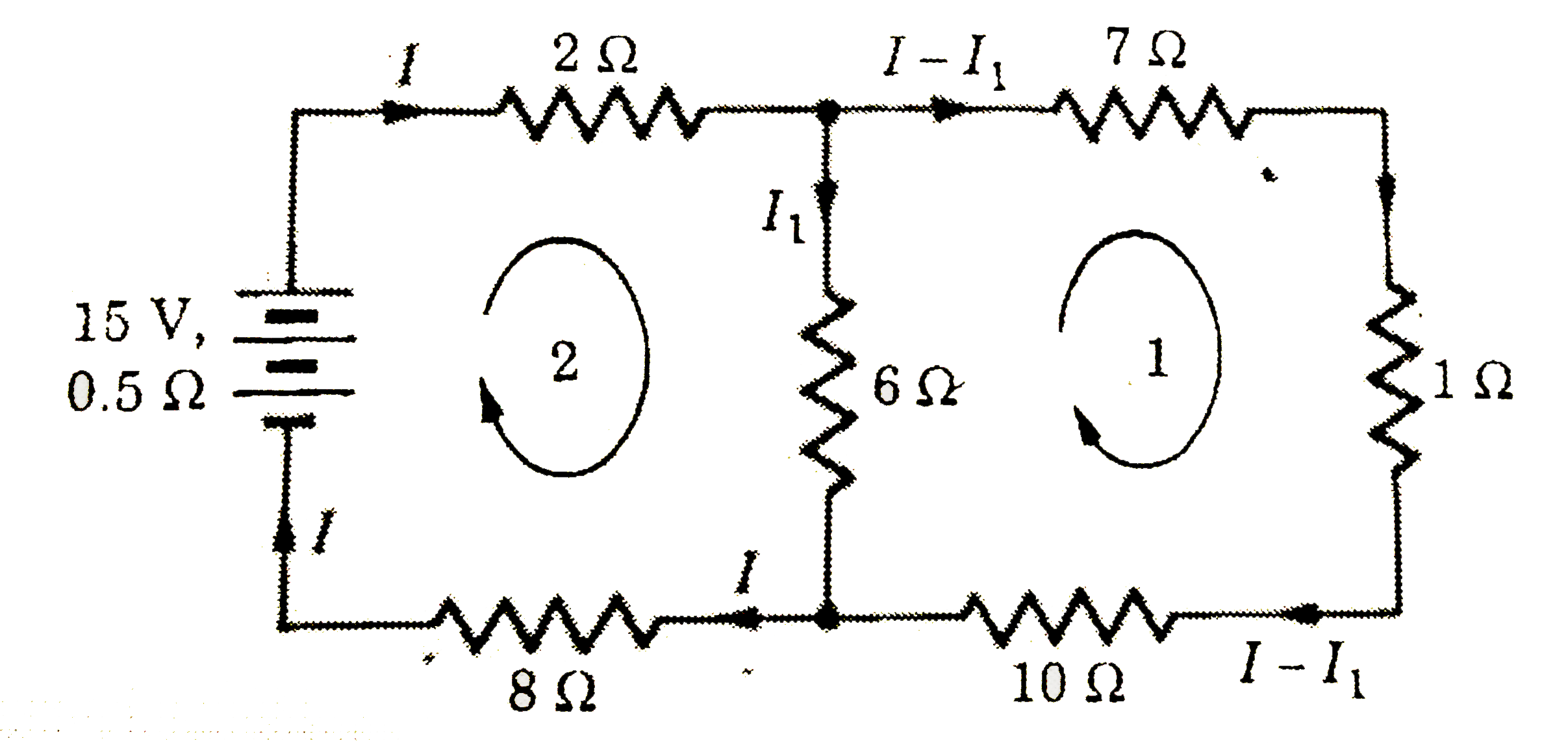
View SolutionA 5 V battery with internal resistance 2Ω and a 2V battery with internal resistance 1Ω are connected to a 10Ω as shown in the figure.
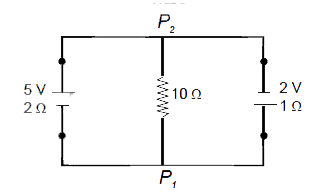
The current in the 10Ω resistance is
View SolutionA wire of uniform cross section of resistance 16Ω is divided into four pieces in the ratio of 1 : 2 : 3 : 4 and ll the four resistros are connected in the form of a square . Calculate the current drawn from the battery, if a battery of emf 10 V and internal resistance 0.5Ω is connected across the resistor with least resistance.
View Solution
