A current in a circuit having constant resistance is tripled. How does this affect the power dissipation?
To solve the problem of how tripling the current in a circuit with constant resistance affects power dissipation, we can follow these steps:
Step 1: Understand the Power Formula
The power (P) dissipated in a circuit can be calculated using the formula:
P=V×I
where V is the voltage and I is the current.
Step 2: Relate Voltage to Current and Resistance
According to Ohm's Law, the voltage (V) across a resistor is given by:
V=I×R
where R is the resistance.
Step 3: Substitute Voltage in the Power Formula
Substituting the expression for voltage into the power formula, we get:
P=(I×R)×I=I2×R
Step 4: Analyze the Effect of Tripling the Current
If the current is tripled, the new current I′ can be expressed as:
I′=3I
Now, substituting this into the power formula:
P′=(I′)2×R=(3I)2×R=9I2×R
Step 5: Compare the New Power with the Original Power
The original power P was:
P=I2×R
The new power P′ is:
P′=9I2×R
Thus, we can see that:
P′=9P
Conclusion
Therefore, when the current in the circuit is tripled, the power dissipation increases by a factor of 9.
---
The power (P) dissipated in a circuit can be calculated using the formula:
P=V×I
where V is the voltage and I is the current.
According to Ohm's Law, the voltage (V) across a resistor is given by:
V=I×R
where R is the resistance.
Substituting the expression for voltage into the power formula, we get:
P=(I×R)×I=I2×R
If the current is tripled, the new current I′ can be expressed as:
I′=3I
Now, substituting this into the power formula:
P′=(I′)2×R=(3I)2×R=9I2×R
The original power P was:
P=I2×R
The new power P′ is:
P′=9I2×R
Thus, we can see that:
P′=9P
Therefore, when the current in the circuit is tripled, the power dissipation increases by a factor of 9.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Knowledge Check
In the series LCR circuit, the power dissipation is through
ARBLCCDBoth L and CIn an a.c. circuit with voltage V and current I, the power dissipated is
AVIB12VIC1√2VIDdepends on the phase between V and IA sinusoidal A.C. current flows through a resistor of resistance R. If the peak current is IP, then the power dissipated is
AI2pRcosθB12I2pRC4πI2pRD1πI2pR
Assume that the batteries in figure have negligible internal resistance. Find
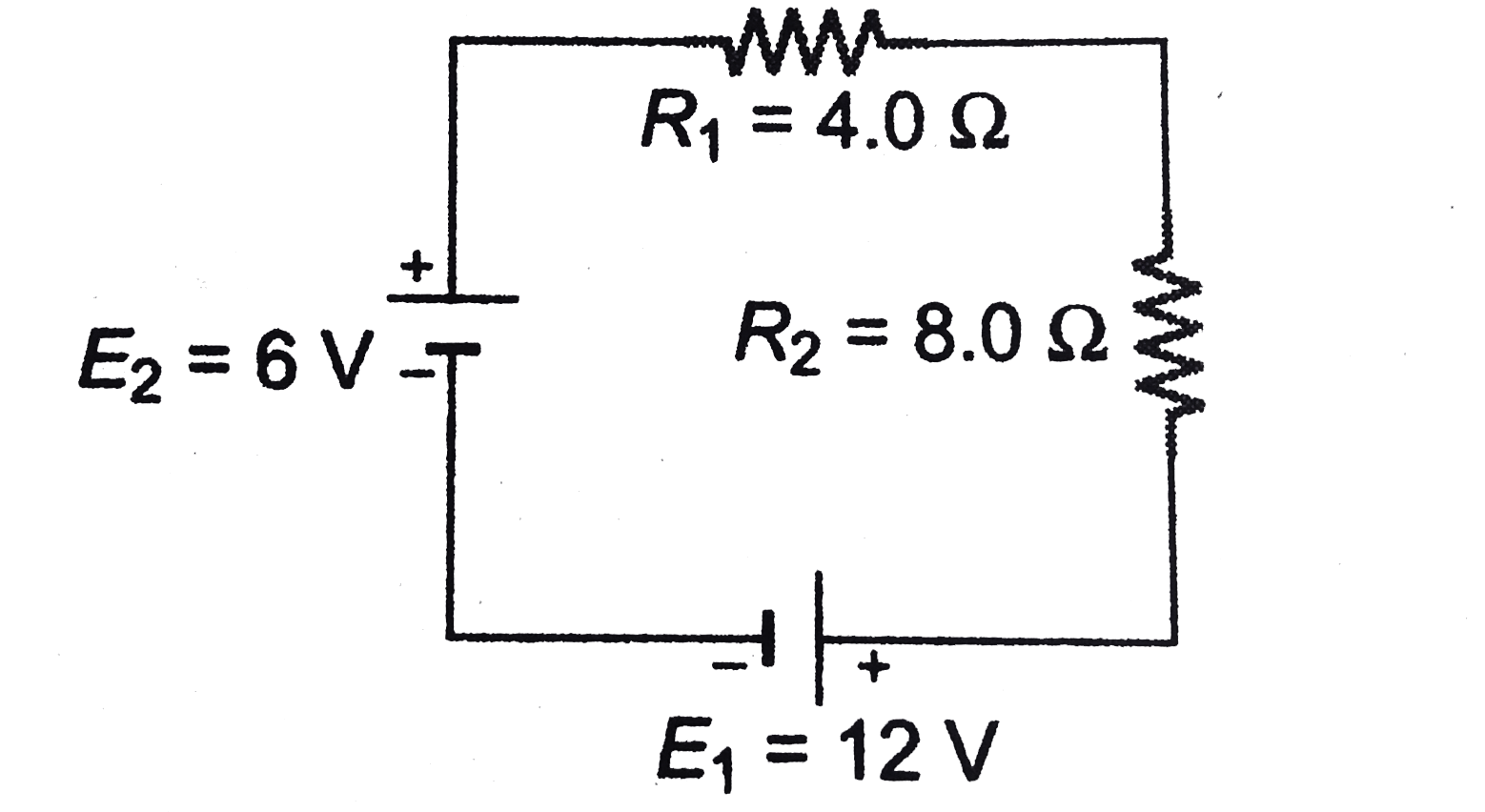
a. the current in the circuit,
(b) the power dissipated in each resistor and
(c) the power of each battery, stating whether energy is supplied by or absorbed by it
View SolutionIf V0 and I0 are the peak current and voltage across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionWhen V = 100 sinωt is applied across a series (R-L-C) circuit, At resonance the current in resistance (R=100ohm) is i = i0 sinωt, then power dissipation in circuit is:-
View SolutionIn an AC circuit with voltage V and current I, the power dissipated is
View Solution

